[R] 눈으로 확인하는 중심극한정리

통계학을 공부하신 분이라면 한 번쯤 중심극한정리(Central Limit Theorem, CLT)라는 용어를 들어보셨으리라 생각합니다. 중심극한정리는 추론통계학의 핵심이 되는 정리 중의 하나인데, 이 정리를 통계학에서 쓰는 기호와 용어를 이용해 설명하면 아래와 같습니다.

평균이 \(\mu\) 이고 분산이 \(\sigma^2\) 인 모집단으로부터 추출한 크기가 \(n\)인 확률표본의 표본평균 \(\bar{X}\)는 \(n\)이 증가할수록 모집단의 분포유형에 상관없이 근사적으로 정규분포 \(N(\mu, \sigma/n)\)을 따른다.

중심극한정리에 의하면 모집단의 분포가 연속형이든, 이산형이든, 또는 한쪽으로 치우친 형태이든 간에 표본의 크기가 클수록 표본평균의 분포는 근사적으로 정규분포에 근접한다는 이야기입니다. 일반적으로 여러 통계분석기법에서 분석모형에 대한 정규성 가정을 하는데 이러한 가정은 중심극한정리를 바탕으로 이루어진 것입니다.

정말 그런지 R을 이용해 눈으로 직접 확인해 보도록 하겠습니다. 먼저, 다음과 같이 함수를 정의합니다.

> CLT.plot <- function(r.dist, n, ...) {
+  
+   means <- double()
+  
+   # 사이즈 n의 샘플을 500회 생성하여 표본평균을 계산
+   for(i in 1:1000) means[i] = mean(r.dist(n,...))
+  
+   # 표본평균을 표준화
+   std.means <- scale(means)
+  
+   # 플롯의 파라메터 설정(2개의 플롯을 한 화면에)
+   par(mfrow = c(1, 2))
+  
+   # 히스토그램과 표본의 밀도
+   hist(std.means, prob = T, col = "light grey",
+       border = "grey", main = NULL, ylim = c(0, 0.5))
+   lines(density(std.means))
+   box()
+  
+   # 표준정규분포 곡선
+   curve(dnorm(x, 0, 1), -3, 3, col = 'blue', add = T)
+  
+   # Q-Q plot
+   qqnorm(std.means, main="", cex = 0.8)
+   abline(0, 1, lty = 2, col = "red")
+   par(mfrow = c(1, 1))
+ }

먼저 대표적인 비대칭 분포의 하나인 카이제곱 분포의 자유도 1의 경우를 살펴보도록 하겠습니다. 아래와 같이 카이제곱 분포를 따르는 임의의 값을 생성하는 rchisq() 함수를 이용하여,

• 카이제곱 분포, df=1, n=1

> CLT.plot(rchisq, n = 1, df = 1)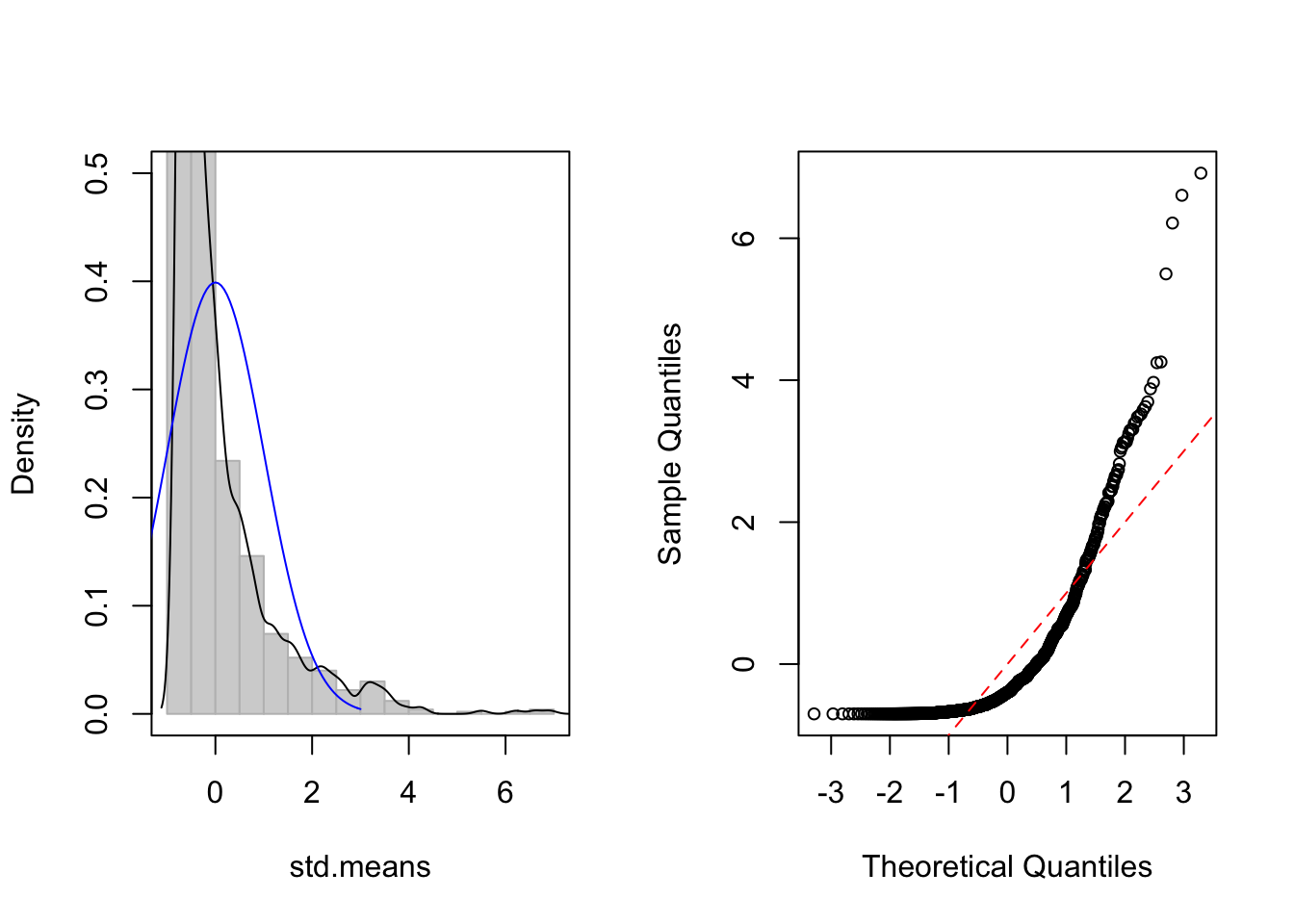

• 카이제곱 분포, df=1, n=10

> CLT.plot(rchisq,n = 10, df = 1)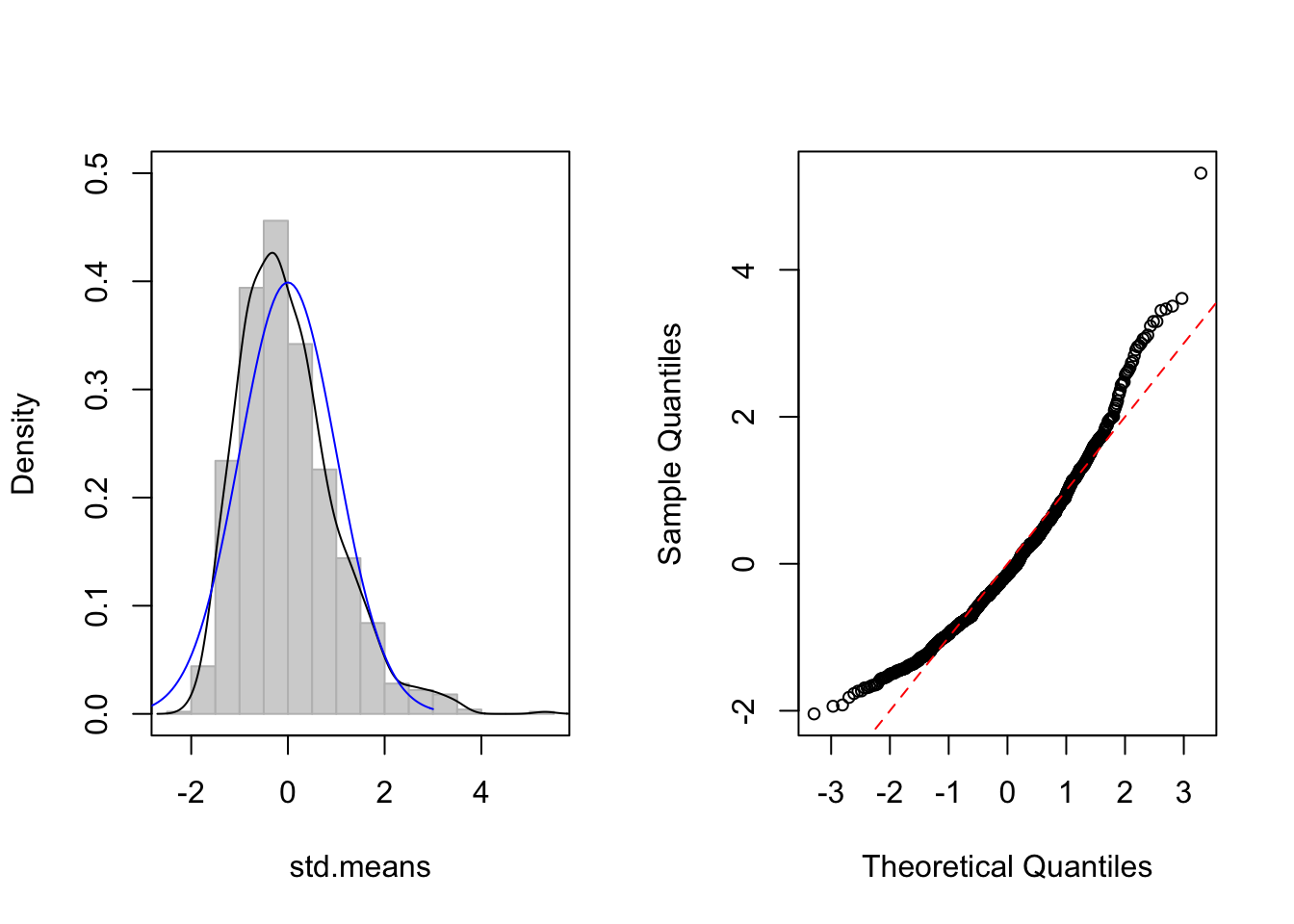

• 카이제곱 분포, df=1, n=50

> CLT.plot(rchisq, n = 50, df = 1)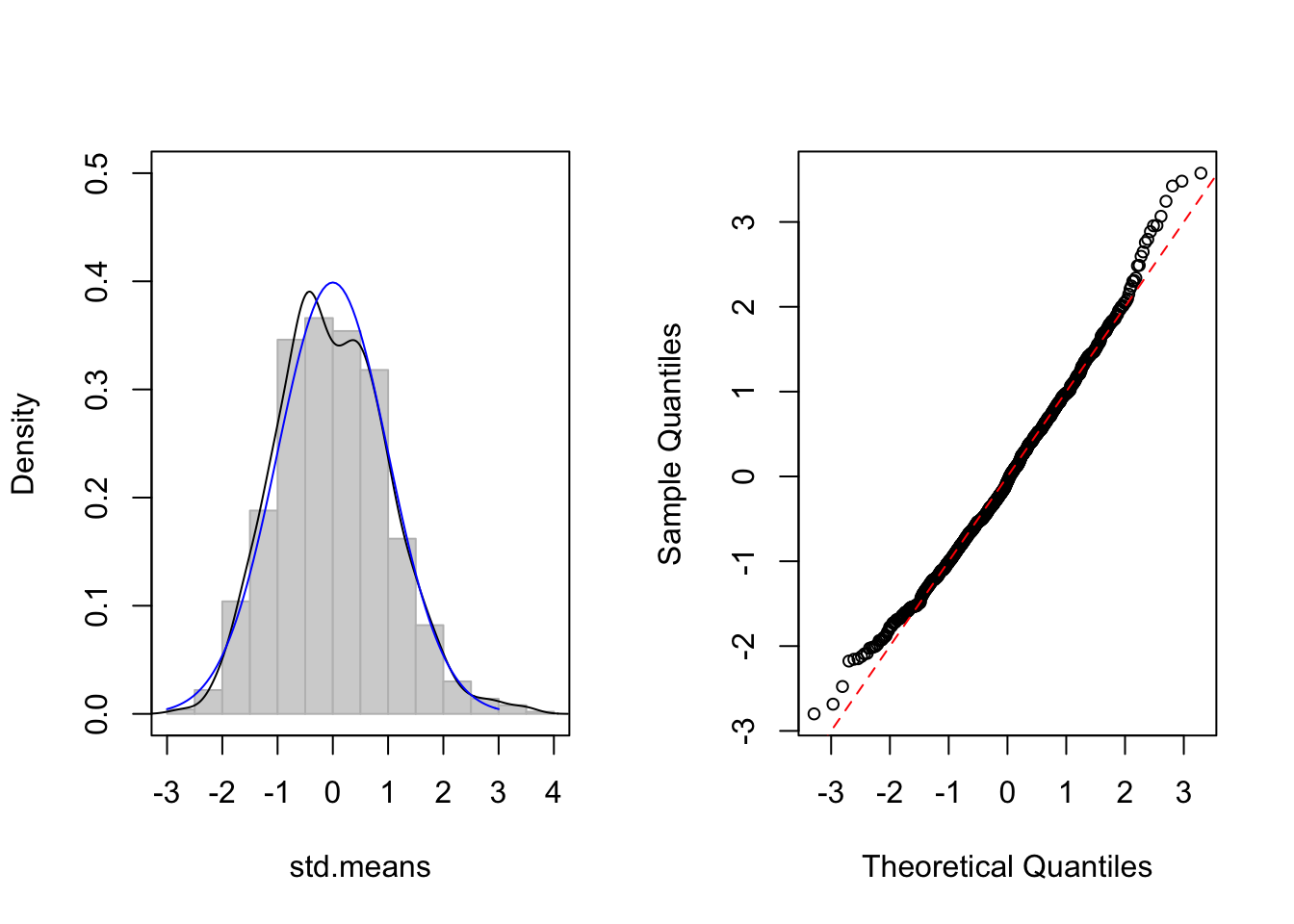

두 번째로 역시 대표적인 이산형 분포의 하나인 이항분포의 경우, rbinom() 함수를 이용하여,

• 이항분포, size=10, p=0.5, n=1

> CLT.plot(rbinom, n = 10, size = 10, p = .5)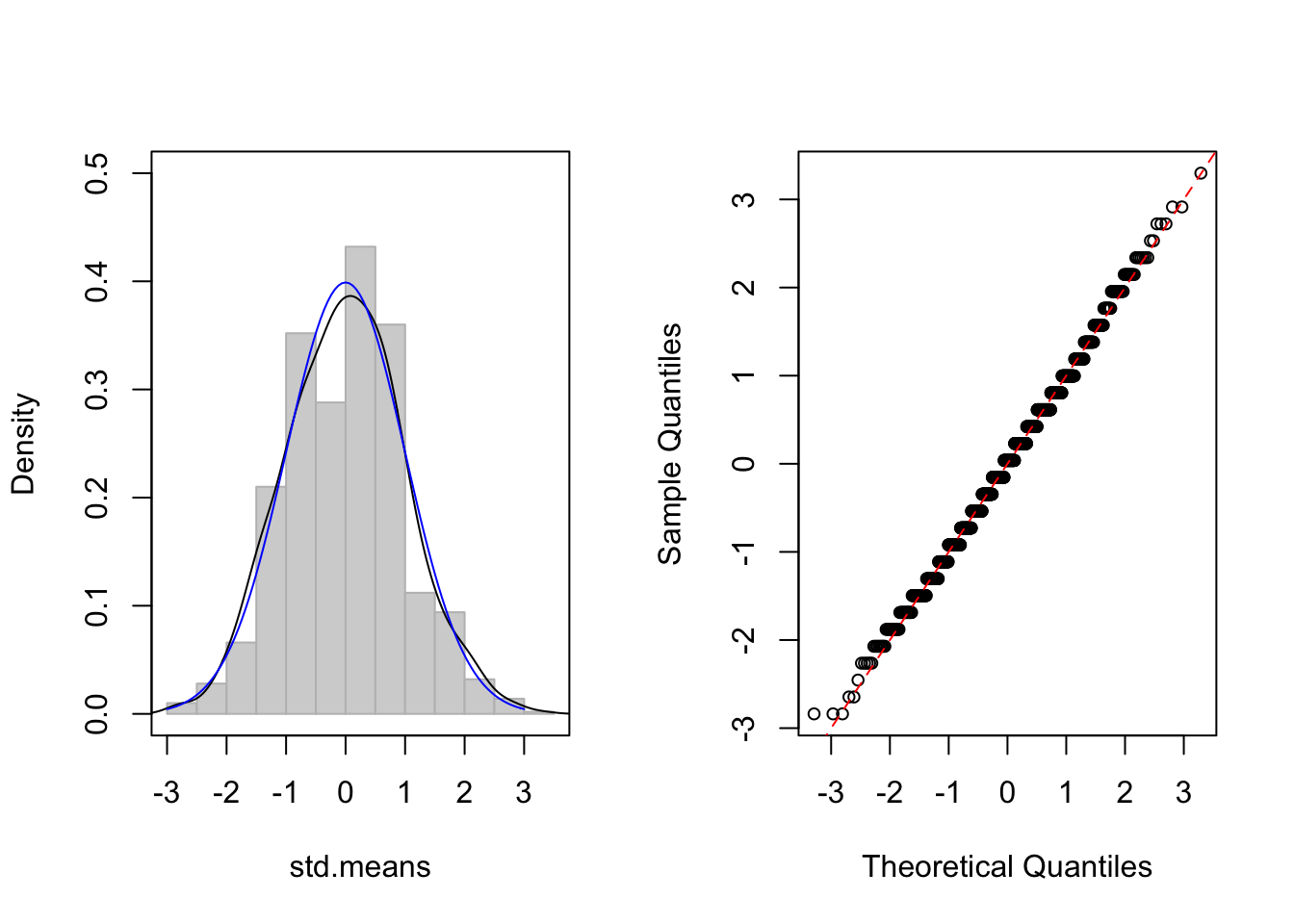

• 이항분포, size=10, p=0.5, n=10

> CLT.plot(rbinom, n = 10, size = 10, p = .5)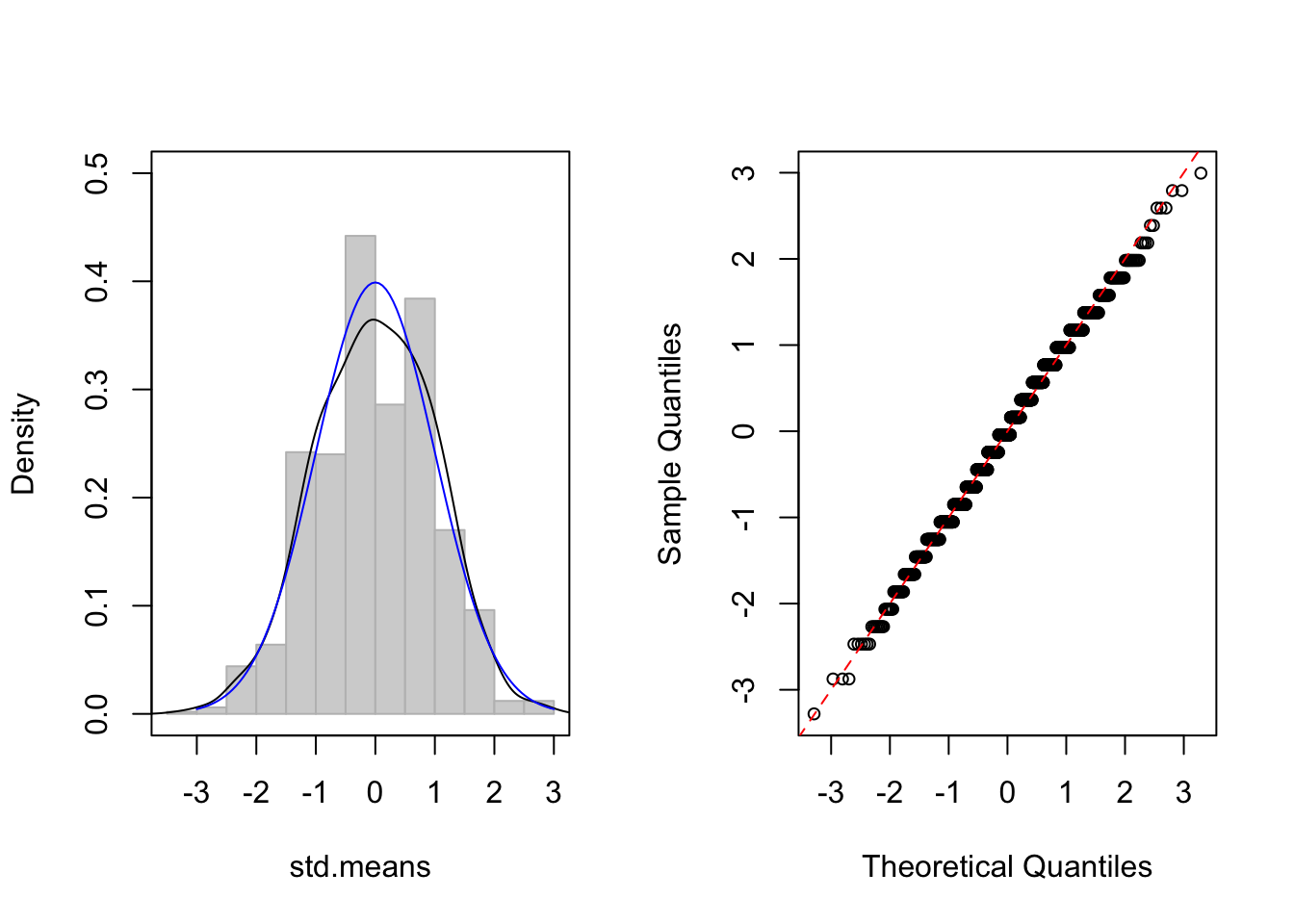

• 이항분포, size=50, p=0.5, n=50

> CLT.plot(rbinom, n = 50, size = 10, p = .5)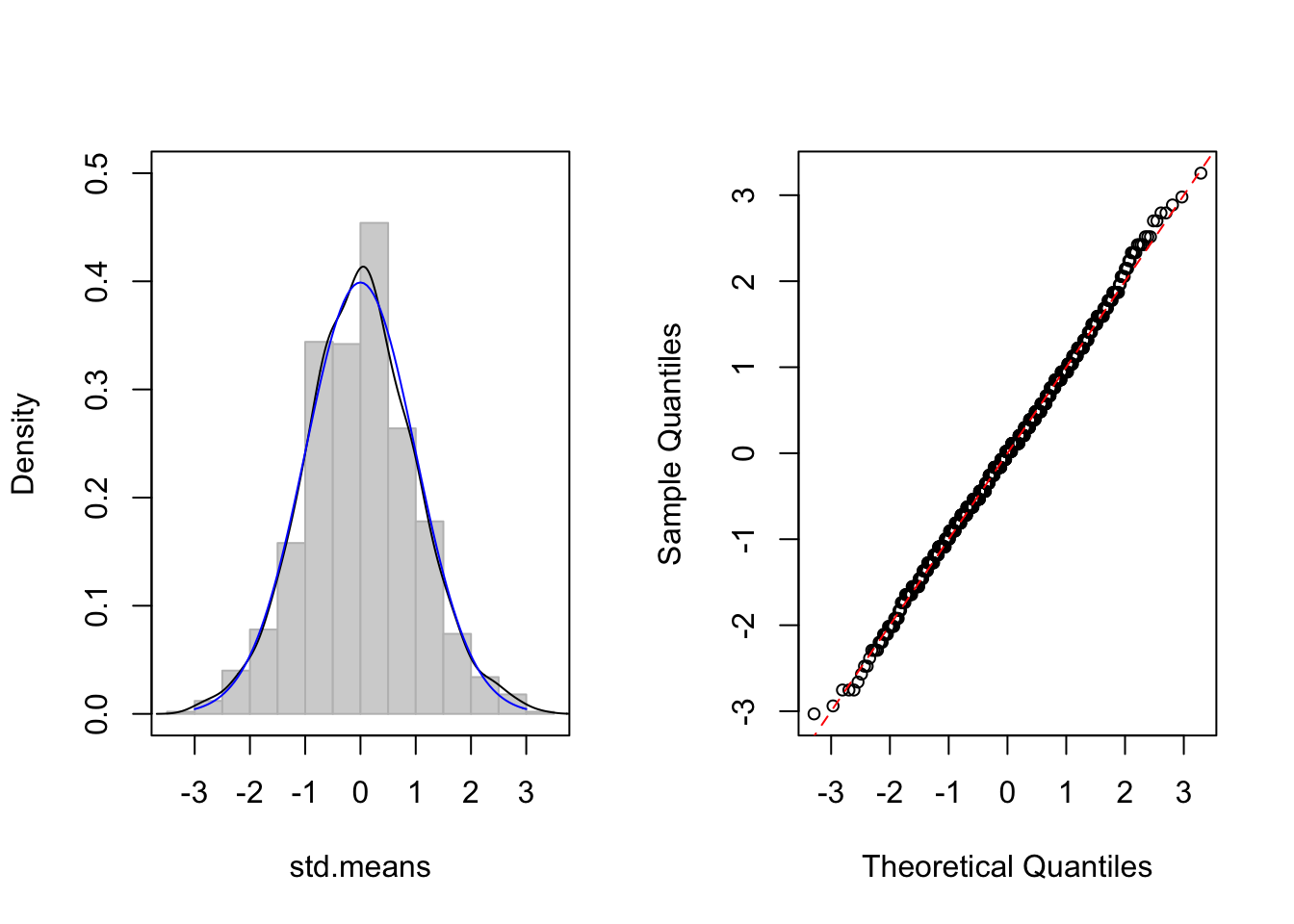

보시는 바와 같이 샘플사이즈 n 이 커질수록 파란색 실선인 정규 분포에 점점 가까워져 감을 알 수 있습니다. 물론 수학적인 증명도 중요합니다. 하지만, 이렇게 눈으로 직접 확인하는 방법이 조금이라도 쉽게 통계이론을 이해하는 데 도움이 되리라 생각합니다.