1980년대와 2000년대 프로야구 투수들의 방어율 어느 쪽이 낮을까?

프로야구 좋아하세요? 저도 즐겨 보는 편입니다.
일본에 와서는 아무래도 우리나라 선수들이 활약하는 팀의 경기를 관심 있게 보곤 합니다. 이승엽 선수가 요미우리 자이언츠에 소속되어 있을 때, 직장 동료들과 도쿄 돔에 갔었는데 마침 이승엽 선수가 2루타로 타점을 올리고 팀이 승리해서 으쓱했던 기억도 나네요.

우리나라의 프로야구는 아시다시피 1981년 처음 시작되었습니다. 그땐 저도 꼬맹이 초등학생이었는데 벌써 30년이 지났네요. 당시의 쟁쟁했던 선수들이 이제는 감독이 되어 팀을 지도하는 모습을 보니 감회가 새롭습니다. 그때나 지금이나 저는 두산 팬입니다. 박철순 선수의 활약이 아직도 기억에 많이 남네요.

요즘 프로야구 투수를 보면 그 역할이 세분되어서 선발, 중간계투, 마무리의 구분이 뚜렷합니다. 80년대의 투수들은 한 번 경기에 나오면 꽤 오래 던졌던 것 같았는데 말이죠. 그래서 재미삼아 1980년대 투수들과 2000년대 투수들의 방어율을 통계분석 패키지인 R을 이용해 비교해보았습니다. 이번 비교에 이용한 자료는 한국 프로야구의 통계와 역사를 제공하는 스탯티즈에서 제공하는 투수기록 중 통산 방어율 데이터를 이용하였습니다.

1980년대에 활약했던 투수는 71명이 2000년대에는 109명의 기록이 등록되어 있습니다.
먼저 양 시대의 방어율 분포를 Boxplot을 통해 살펴보면

> pitcher <- read.csv("https://www.dropbox.com/s/lmwbrf3d1ow7om6/pitcher.csv?dl=1")
> boxplot(ERA ~ Decade, data = pitcher, col = c("darkred", "darkblue"),
+         main = "ERA Distribution")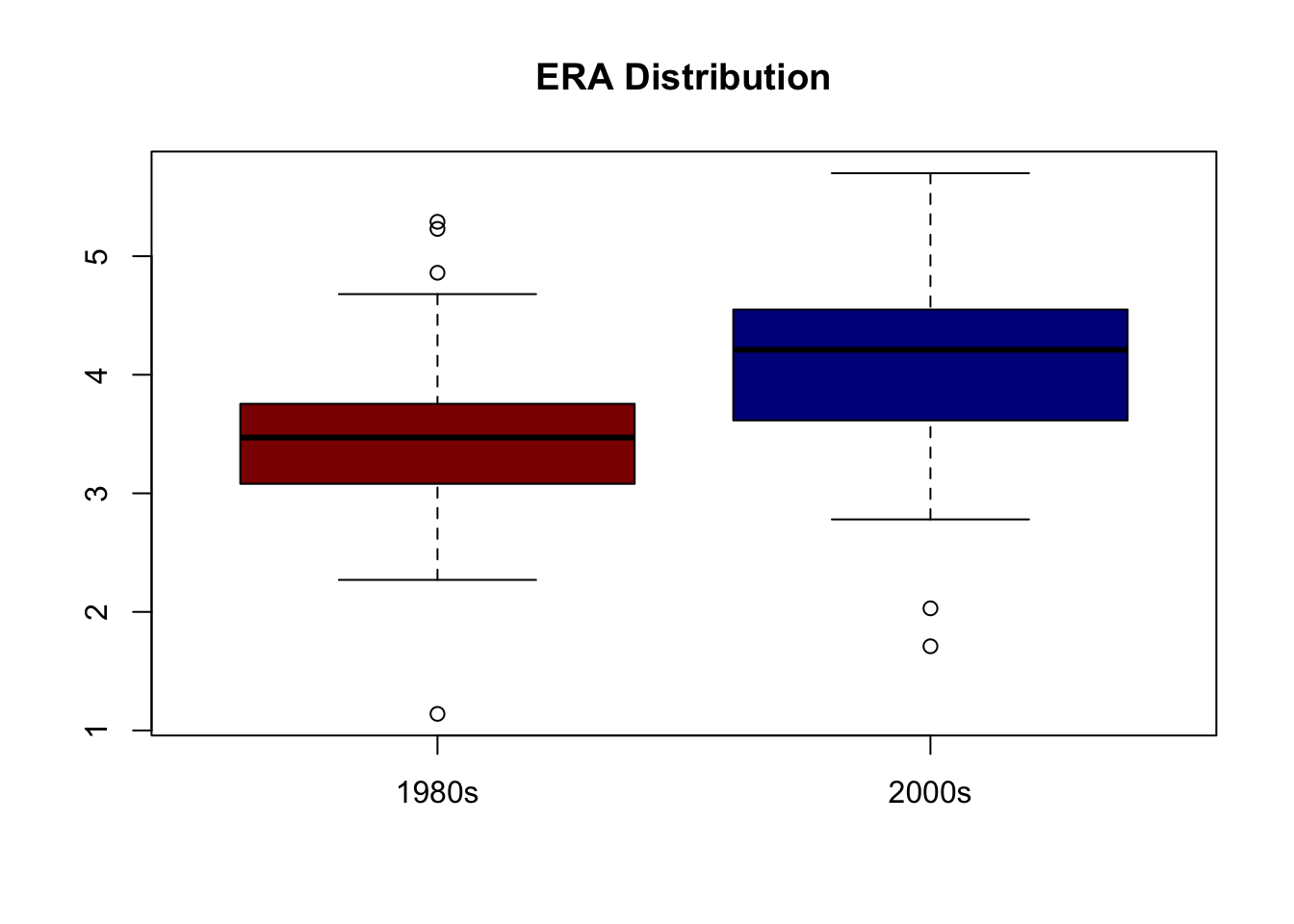

2000년대 타자들의 기술과 수준이 높아진 이유일까요? 아니면 1980년대 투수들의 능력이 우수했던 걸까요? 위 그림을 보면 1980년대 투수들의 방어율이 2000년대 투수들보다 비교적 낮음을 알 수 있습니다. 그렇다면 통계적으로 양 시대 투수들의 평균방어율은 차이가 있다고 할 수 있을까요? 두 표본집단의 평균비교를 위한 t-검정을 통해 통계적 유의성을 알아보도록 하겠습니다. 두 표본집단의 분산이 같을 때와 서로 다를 때 t-검정의 방법은 약간 달라지는데요. 분산이 같은지 알아보는 방법이 F-분포를 이용한 검정입니다.

> var.test(ERA ~ Decade, data = pitcher)

#> 
#>  F test to compare two variances
#> 
#> data:  ERA by Decade
#> F = 1, num df = 70, denom df = 100, p-value = 1
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#>  0.664 1.538
#> sample estimates:
#> ratio of variances 
#>              0.999

검정 결과 유의확률(p-value)이 0.9898이므로 유의수준 5%에서 두 집단의 분산이 서로 같다는 가설(귀무가설)을 기각하지 못하게 됩니다. 즉, 두 집단의 분산은 같다고 할 수 있습니다. 다음으로, 두 집단의 분산이 같다는 가정하에서 t-검정은

> t.test(ERA ~ Decade, data=pitcher, var.equal=T)

#> 
#>  Two Sample t-test
#> 
#> data:  ERA by Decade
#> t = -6, df = 200, p-value = 1e-09
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#>  -0.861 -0.458
#> sample estimates:
#> mean in group 1980s mean in group 2000s 
#>                3.42                4.08

결과를 보면 1980년대 투수들의 평균 방어율은 3.425, 2000년대 투수들의 평균 방어율은 4.084이고, 검정 결과 유의확률이 매우 낮으므로 통계적으로 1980년대 투수와 2000년대 투수의 평균 방어율은 차이가 있다고 할 수 있습니다.

그런데 앞선 포스팅에서 t-검정은 표본집단에 대해 정규분포의 가정이 성립할 때에만 사용할 수 있다고 했습니다. 과연 양 시대 투수들의 방어율은 정규분포를 따르고 있을까요? 그 분포를 좀 더 자세히 보기 위해 밀도함수를 그려보면 다음과 같습니다.

> par(mfrow = c(2, 1))
> plot(density(pitcher[which(pitcher$Decade == "1980s"), "ERA"]), col = "darkred",
+     main = "1980s ERA Density", xlim = c(0.5, 6.5))
> rug(pitcher[which(pitcher$Decade == "1980s"), "ERA"], col = "green")
> plot(density(pitcher[which(pitcher$Decade == "2000s"), "ERA"]), col = "darkblue",
+     main = "2000s ERA Density", xlim=c(0.5, 6.5))
> rug(pitcher[which(pitcher$Decade == "2000s"), "ERA"], col="green")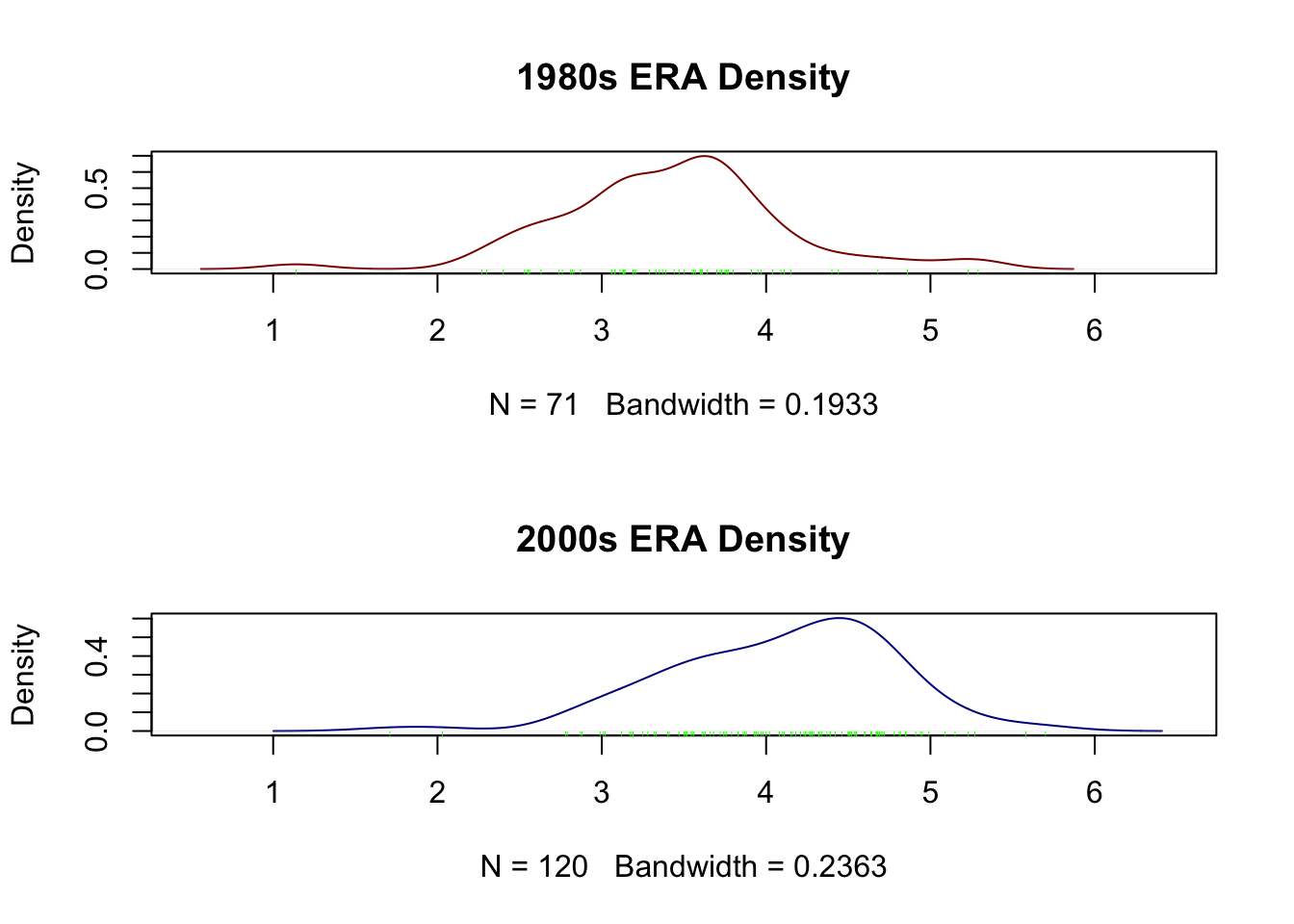

> par(mfrow = c(1, 1))

두 집단 모두 분포의 중심이 한쪽으로 치우쳐 있어서 정규분포를 따른다고 하기에는 약간 모호하기도 하네요. 이럴 때는 비모수 검정방법인 Wilcoxon 순위합 검정을 이용하면 되겠죠.

> wilcox.test(ERA ~ Decade, data=pitcher, conf.int=T)

#> 
#>  Wilcoxon rank sum test with continuity correction
#> 
#> data:  ERA by Decade
#> W = 2000, p-value = 8e-10
#> alternative hypothesis: true location shift is not equal to 0
#> 95 percent confidence interval:
#>  -0.90 -0.51
#> sample estimates:
#> difference in location 
#>                  -0.71

Wilcoxon 순위합 검정도 t-검정의 결과와 마찬가지로 양 시대 투수들의 방어율은 차이가 있다고 할 수 있습니다.

결론을 말하자면 수치상 1980년대 투수들의 평균 방어율이 2000년대 투수들의 평균 방어율보다 낮음을 알 수 있었습니다.

프로야구 이야기인 줄 알고 글을 읽으신 분들께는 죄송합니다. 통계 이야기가 주가 되어 버렸네요.
그냥 중간은 건너뛰시고 결과가 그렇구나~~라고 이해해 주시길…