연쇄(genetic linkage)와 재조합비율(recombination fraction)

멘델의 독립법칙은 두 유전자 좌(genetic locus)의 allele 전달에 관한 법칙입니다만, 독립의 법칙은 두 유전자 좌가 서로 다른 염색체 위에 있을 때만 성립합니다. 두 유전자 좌가 같은 염색체 위에 존재할 때에는 독립의 법칙이 성립하지 않을 때도 있습니다. 두 유전자 좌 간에 독립 법칙이 성립하지 않을 때 두 유전자 좌는 연쇄상태(genetic linkage)에 있다고 합니다. 다시 말하면, 연쇄(genetic linkage) 법칙은 멘델의 유전 법칙 중 독립 법칙의 예외에 해당합니다.

통계학과 유전학의 용어를 이용하여 연쇄의 법칙을 풀어쓰면,

두 유전자 좌가 같은 염색체 위의 근방에 위치하는 경우 한쪽 유전자 좌의 allele이 다음 세대에 전달될 때 또 다른 유전자 좌의 allele은 확률 1/2이 아닌, 두 유전자 좌 사이의 재조합비율(recombination fraction)에 의해 결정되는 확률로 다음 세대에 전달된다.

여기서 잠깐 교차(crossing over)와 재조합(genetic recombination)에 대해서 알아보도록 하겠습니다. 교차란 생식세포의 감수분열 과정에서 일어나는 염색체의 접합에 의해 일어나는 현상으로 접합한 염색체 일부가 서로 뒤바뀌는 것을 말하고, 재조합은 세포분열이 끝난 후의 두 유전자 좌를 측정했을 때의 상태에 대한 개념입니다.

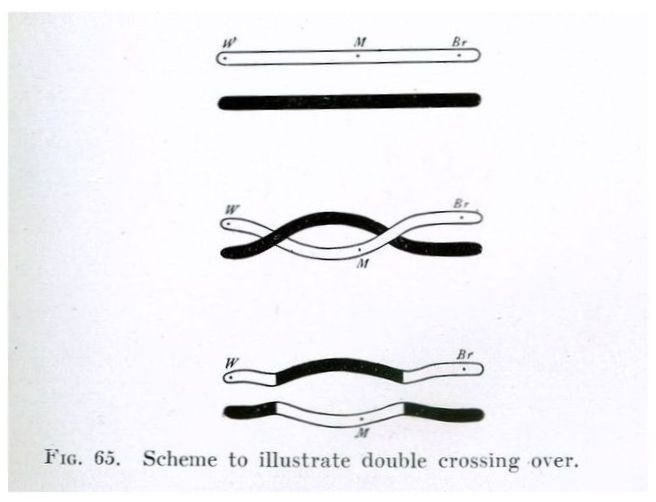
Thomas Hunt Morgan’s A Critique of the Theory of Evolution (1916)

염색체 연쇄의 연구에 커다란 공헌을 한 Thomas Hunt Morgan의 논문에 실린 그림을 예로 설명해 보죠. 세포의 감수분열 전의 염색체 상태는 가장 위의 그림이 되고, 감수분열 과정에서 두 번의 교차가 일어났다고 했을 때 염색체의 상태는 가장 아래쪽의 그림이 됩니다. 만약 감수분열 후 유전자 좌 W와 유전자 좌 M을 측정했다고 하면 두 유전자 좌 사이에는 재조합이 있다고 말합니다. 이에 반해 유전자 좌 W와 유전자 좌 Br을 측정했을 때는 재조합이 없다고 말합니다. 즉, 두 유전자 좌 사이에 교차가 홀수 회 일어나면 재조합이 있다고 이야기하고, 교차가 짝수 회 일어났을 때는 재조합이 없다고 이야기합니다. 일반적으로 유전통계학에서 분석의 대상이 되는 것은 교차가 아닌 재조합입니다.

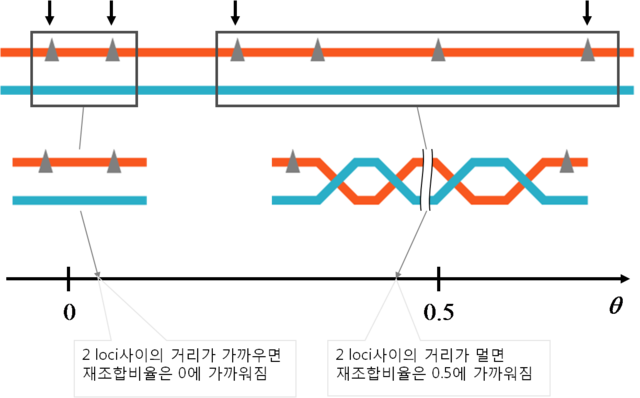
재조합비율은 1회의 감수분열에서 두 유전자 좌 사이에 재조합이 일어날 확률 혹은 다수의 감수분열에서 두 유전자 좌 사이에 재조합이 일어난 감수분열의 비율로 정의됩니다. 통상 재조합비율은 \(\theta\)로 표기하며, \(0 \leq \theta \leq 0.5\)의 값을 가집니다. 또한, \(\theta = 0.5\)일 때 독립의 법칙이 성립합니다.

다시 연사의 법칙으로 돌아가서, 한 개체의 제1 유전자 좌의 유전자형을 Aa, 제2 유전자 좌의 유전자형을 Bb라 할 때, 두 유전자 좌 사이가 연쇄상태에 있다면, allele A와 allele B가 각각 다음 세대에 전달될 확률은

\[ \begin{eqnarray*} P(AB) &\neq& P(A)P(B)=\frac{1}{4} \\ P(A|B) &\neq& P(A) \end{eqnarray*} \]

가 됩니다. 물론 연쇄상태에 있지 않다면 위 식은 독립의 법칙 때의 식과 같게 되어

\[ \begin{eqnarray*} P(AB) &=& P(A)P(B)=\frac{1}{4} \\ P(A|B) &=& P(A) \end{eqnarray*} \]

가 성립하게 됩니다.

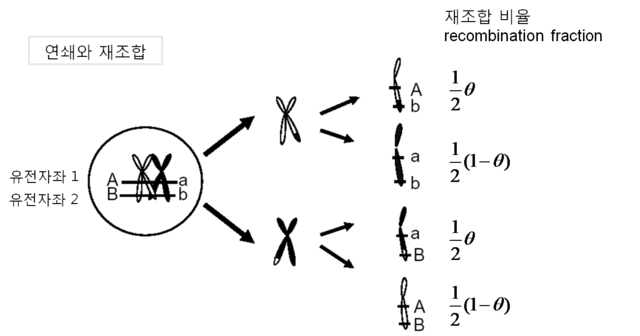
만약 위 식에서 \(P(AB) < 1/4\)라 하고 A-B를 아버지로부터 a-b를 어머니로부터 물려받은 allele라 한다면, 같은 염색체 위에 있는 allele은 A-B 혹은 a-b의 조합(haplotype)이 다음 세대에 전달될 것입니다. 그러나 A-b, a-B라는 allele 조합이 생식체에서 발견된다면 이는 감수분열 시 재조합이 일어났다는 것을 의미합니다. 따라서 연쇄의 법칙은 부모로부터 자식으로 전달되는 allele에 대해,

\[ P(a|B)=P(A|b)=\theta \]

가 성립하는 것을 의미합니다. 또한,

\[ \begin{eqnarray*} P(A|B) & = & 1-P(a|B) \\ P(a|b) & = & 1-P(A|b) \end{eqnarray*} \]

이므로, \(P(A \mid B) = P(a \mid b) = 1-\theta\)가 됩니다.

앞서 설명한 멘델의 유전법칙과 함께 연쇄의 법칙은 유전통계학을 공부할 때 가장 기본이 되고 중요한 법칙들입니다. 이 법칙들을 이용하여 질환의 원인이 되는 유전자를 찾아 내는 방법 중의 하나가 바로 연쇄분석(linkage analysis)입니다.