[유전통계] 통계로 설명하는 멘델의 유전 법칙

1) 우열의 법칙(law of dominance)

우열의 법칙은 유전자형(genotype)과 표현형(phenotype)의 대응관계에 관한 법칙으로 사실은 가장 정의하기 어려운 법칙입니다. 표현형에는 질적 표현형(qualitative phenotype)과 양적 표현형(quantitative phenotype)이 존재하며. 완두콩의 색, 완두콩의 모양, 질병의 여부 등과 같이 카테고리로 나눌 수 있는 표현형이 질적 표현형에, 사람의 키, 몸무게 등과 같이 카테고리로 나눌 수 없는 표현형이 양적 표현형에 해당합니다.

우열의 법칙에 대한 가장 간단한 예가 질적 표현형의 완전우성, 완전열성의 경우입니다. 즉, 유전자형을 구성하는 두 개의 대립형질(allele) 중 질병의 원인이 되는 대립형질을 A, 또 하나의 대립형질을 a라 한다면, 유전자형이 AA, Aa일때 반드시 병에 걸리는 경우가 완전우성, AA 일 때만 병에 걸리고Aa, aa일 때는 병에 걸리지 않는 경우가 완전 열성입니다. 이를 확률로 바꿔 말하면 “병에 걸릴 확률이 1, 병에 걸리지 않을 확률이 0″과 같이 표현할 수 있습니다. 그러나 실제로는 완전우성이나 완전열성은 드물고, 유전자형에 따라 병에 걸릴 확률이 변하게 되는 경우가 많습니다. 이를 불완전 침투(incomplete peretrance)라 하고, 병에 걸릴 확률을 침투율이라 합니다.

우열의 법칙을 통계학에서 쓰는 용어로 설명하면 다음과 같습니다.

질환과 관련한 allele을 A라 하고, 또 다른 allele를 a라 한다면 AA, Aa, aa 3가지의 유전자형이 존재한다. 이때, 하나의 실험 “어떤 개인이 부모로부터 각각 하나의 allele를 전달받아 하나의 유전자 좌(genetic locus)를 결정하고, 그 유전자형하에서 병에 걸리거나(D) 혹은 병에 걸리지 않게 된다(U).”를 정의할 수 있다. 이때 확률함수(침투율)는

\[ \begin{align*} P(D|AA) &=& p_{AA}, \\ P(D|Aa) &=& p_{Aa}, \\ P(D|aa) &=& p_{aa} \end{align*} \]

단, \(p\_{AA}, p\_{Aa}, p_{aa}\) 는 각각 AA, Aa, aa의 침투율(발병확률).

양적 표현형에서는 확률함수가 아닌 확률밀도함수로서 표현되므로 양적 표현형의 밀도함수가 정규분포를 따른다고 하면, 확률변수 X의 분포는

\[ \begin{align*} X: AA & \sim & N(\mu_1, \sigma_1^2) \\ X: Aa & \sim & N(\mu_2, \sigma_2^2) \\ X: aa & \sim & N(\mu_3, \sigma_3^2) \end{align*} \]

를 따른다.
즉, 표현형의 분포는 유전자형에 의해 결정된다.

이를 그림으로 정리하면 다음과 같습니다.

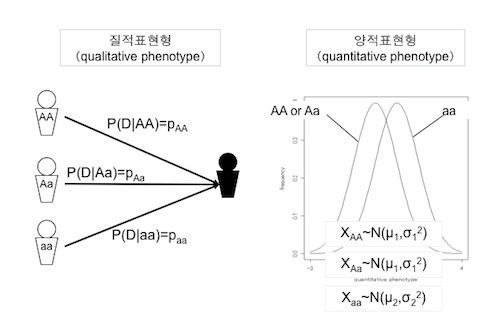
단, 위의 그림에서 왼쪽은 질적 표현형의 유전자형 계승양식의 예를, 오른쪽은 양적 표현형의 우성 계승양식을 예로 들었습니다.

2) 분리의 법칙(law of segregation)

분리의 법칙은

개체의 유전자형을 구성하는 2개의 대립형질(allele)은 같은 확률로 부모로부터 자식에게 전달되며, 부모 유래의 allele 조합이 다음 세대의 유전자를 결정한다.

라는 법칙입니다.
분리의 법칙을 그림으로 설명하면 다음과 같습니다.

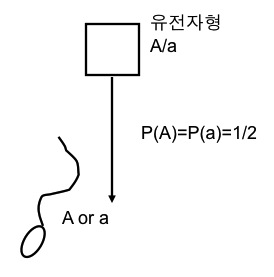
즉, 아버지(혹은 어머니)로부터 하나의 allele가 1/2의 확률로 다음 세대에 전달된다는 이야기죠. 다시 말해 분리의 법칙은 유전자형을 구성하는 allele가 무엇이든, 나이에 상관없이, 성별에 상관없이, 형제자매에게 어떤 allele가 전달되든 상관없이, 비가 오든, 바람이 불든 상관없이 부모로부터 특정 allele가 자식에게 전달될 확률은 1/2 이란 이야기입니다.

인간은 아버지, 어머니로부터 각각 하나의 allele를 전달받게 되므로, 아버지의 유전자형이 Aa, 어머니의 유전자형이 Aa라면 자식의 유전자형이 AA, Aa, aa가 될 확률은 각각,

\[ \begin{align*} P(AA) & = & P(A) \times P(A) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \\ P(Aa) & = & P(A) \times P(a) + P(a) \times P(A) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \\ P(aa) & = & P(a) \times P(a) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \end{align*} \]

가 됩니다.

3) 독립의 법칙(law of independent assortment)

분리의 법칙이 하나의 유전자 좌(genetic locus or locus; 복수형은 loci)의 allele 전달에 관한 법칙이라면, 독립의 법칙은 복수의 유전자 좌의 allele 전달에 대한 법칙입니다. 더욱이 독립의 법칙이 성립하기 위해서는 전달에 관계하는 모든 유전자 좌가 서로 다른 염색체에 위치해야 합니다. 독립의 법칙은

2개의 유전자 좌(1)가 서로 다른 염색체상에 있을 때 하나의 유전자형을 구성하는 두 개의 allele 중 하나가 다음 세대에 전달될 때, 또 다른 유전자 좌(2)의 allele는 유전자 좌(1)가 어떤 allele를 전달했는가에 상관없이 같은 확률로 다음 세대에 전달된다.

는 법칙입니다.

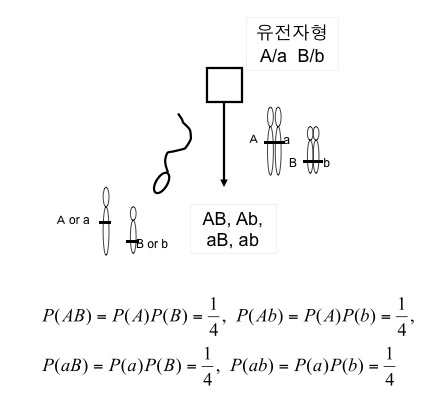
독립의 법칙은 세포의 감수분열(생식세포 분열)에서 상동염색체의 움직임과 관련이 있습니다. 한 쌍의 상동염색체가 두 개의 딸세포로 분리의 법칙에 의해 같은 확률로 분리되지만, 서로 다른 염색체의 상동염색체의 분리방법은 서로 영향을 주지 않는다는 법칙입니다.

만약 2개의 유전자 좌가 같은 염색체 위에 위치한다면 어떻게 될까요? 이 같은 경우는 독립의 법칙을 따르지 않고 연관(linkage)을 가지게 됩니다. 이 연관은 유전통계학에서 매우 중요한 개념이므로 따로 포스팅 하도록 하겠습니다.