[유전통계학] 재조합비율과 거리

재조합비율(recombination fraction)은 한 번의 감수분열에서 두 유전자 좌 사이에 재조합이 일어날 확률로 정의됩니다. 확률이므로 0에서 1 사이의 값을 가지는 것이 당연하지만 통상 $0\le \theta \le 0.5$의 값을 가집니다. 이는 유전자 좌 사이가 멀리 떨어져 있으면 교차로 인해 재조합이 일어날 확률이 높아지지만 또 한 번 교차가 일어나 재조합이 한 번 더 일어날 확률도 높아지기 때문입니다.

드물게 $\theta >0.5$일 때가 있는데, 이는 첫 번째 재조합이 일어났을 때, 두 번째 재조합이 억제되는 간섭(interference)이라는 현상 때문입니다.

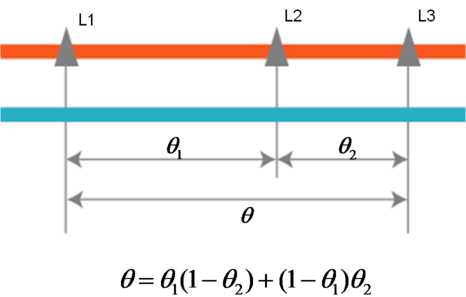
재조합비율은 염색체위의 두 유전자 좌의 거리가 멀수록 큰 값을 가지기 때문에 거리의 개념과 비슷하지만, 확률이기 때문에 1 이상의 값을 가지지 못하므로 일반적인 거리의 개념과는 차이가 있습니다. 예를 들어, 다음 그림과 같이 L1, L2, L3 3개의 유전자 좌가 같은 염색체 위에 있고 L1, L2 사이의 재조합 비율을 ${\theta }_1$, L2, L3 사이의 재조합비율을 ${\theta }_2$라 한다면, L1과 L3 사이의 재조합 비율 $\theta$은 ${\theta }_1+{\theta }_2$가 되지 않습니다. 즉, 확률이기 때문에 단순 덧셈이 아닌 L1과 L2 혹은 L2와 L3의 어느 한 쪽에서만 재조합이 일어나야만 하므로

$$\theta ={\theta }_1(1-{\theta }_2)+{\theta }_2(1-{\theta }_1)$$

가 됩니다.

재조합 비율은 확률이기 때문에 두 유전자 좌 사이의 거리를 나타낼 척도가 필요합니다. 일반적으로 유전적 거리(genetic map distance)와 물리적 거리(physical map distance)를 많이 사용합니다. 유전적 거리는 두 유전자 좌사이에 일어날 교차의 횟수의 기댓값으로 정의합니다. 단위는 M(morgan)으로 표시합니다. 즉, 1M은 한 번의 감수분열에서 한 번의 교차가 일어날 것으로 기대되는 거리를 말하며 덧셈이 가능합니다. 두 유전자 좌의 거리가 떨어져 있으면 교차의 수도 비례적으로 늘어나므로 이론적으로 유전적 거리는 0에서 무한대의 값을 가집니다.

또한, 두 유전자 좌 사이의 염기 수를 물리적 거리라고 하며 단위는 bp(base pair)입니다. 유전적 거리와 물리적 거리는 그 순서 이외에는 특별한 관련이 없으며, 유전통계학에서는 그다지 중요시하지 않는 척도입니다.

사람의 모든 상동염색체의 유전적 거리는 남성이 약 28M, 여성이 약 43M, 평균 36M으로 알려져 있습니다. 즉, 여성의 감수분열이 남성보다 재조합이 많습니다. 사람의 물리적 거리는 약 30억bp($3 10^9 $)이므로 1M는 약 ${10}^8$, 1cM(centimorgan)은 ${10}^6$이 되어 1Mbp(mega base pair)에 상당하게 됩니다.

두 유전자 좌 사이의 유전적 거리 $x$와 재조합비율 $\theta$의 관계를 표현한 함수를 지도함수(map function)라 합니다. 유전자 좌 사이에서 일어나는 교차의 수가 포아송 분포를 따른다고 가정하면 Haldane의 지도함수는

$$x=-\frac{1}{2}\log (1-2\theta )$$

가 되고, 그 역은

$$\theta =-\frac{1}{2}(1-e^{-2x})$$

가 됩니다. 재조합비율과 유전적 거리의 관계를 Haldane의 지도함수를 이용해 그래프로 나타내면 다음과 같습니다.