GWAS로 배우는 유전통계학 - 2.1 가계모순과 하디-베인베르크 평형 법칙

2.1 가계모순과 하디-베인베르크 평형의 법칙

인간은 부모로부터 각각 하나의 allele를 유전계승법칙에 따라 물려받습니다. 따라서 만약 관측한 유전자형 데이터가 유전계승법칙과 맞지 않다면 관측 데이터가 잘못된 경우가 많습니다. 예를 들어 다음 그림과 같은 가계정보와 하나의 SNP좌위의 유전자형이 관측되었다면

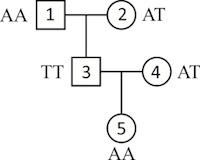
개체 3은 멘델의 분리법칙에 의해 개체 1로부터 allele A를 개체 2로부터 allele A 혹은 T를 물려받게 됩니다. 따라서 유전자형은 AA 혹은 AT가 되어야 합니다. 물론 개체 1이 감수분열(meiosis)할 때 돌연변이(mutation)가 일어날 수도 있습니다. 또, 개체 5는 개체 3과 개체 4로부터 각각 하나의 allele를 물려받게 됩니다만 만약 개체 3의 유전자형이 올바르다 한다면 개체 3의 감수분열에도 돌연변이가 일어났다고 생각할 수밖에 없습니다. 그러나 한 좌위에서 돌연변이가 일어날 확률은 한 번의 감수분열당 약 \(10^{-7}\) 정도로 알려져 있기 때문에 2개체가 같은 좌위에서 돌연변이를 일으켰다고는 생각하기 어렵습니다. 그러므로 개체 3의 유전자형은 AT를 가지는 것이 타당합니다. 물론 이와 같은 가계모순 체크는 가게도의 정보가 있어야 하기 때문에 GWAS보다는 연쇄분석에서 주로 이루어집니다.

한편 가계정보가 없어도 집단을 이용해서 유전자형을 평가할 수 있습니다. 이를 위해서는 무작위 교배(random mating)집단일 필요가 있는데요. 무작위 교배집단이란 무작위로 선택된 남녀의 배우자(gamate)를 유전계승법칙에 의해 물려받은 개체집단을 말합니다. 예를 들어 보면 어떤 대학의 신입생 집단, 회사의 건강진단을 받은 집단, 임상시험의 자원 봉사자들의 집단 등은 각 개체 간에 혈연관계가 거의 없는 집단이라고 생각할 수 있기 때문에 무작위 교배집단이라 할 수 있습니다. 이러한 집단의 allele 분포는 세대를 거듭해도 그다지 변화가 없으며 이런 상태를 하디-베인베르크 평형(Hardy-Weinberg equilibrium; HWE)상태에 있다고 말합니다.

수학적으로는 매우 간단한 법칙입니다만 집단유전학의 연구에는 매우 공헌이 큰 법칙이기도 합니다. 하나의 SNP에 2개의 allele A와 T가 존재한다 하고 집단의 유전자형 AA, AT, TT의 도수를 각각 \(n_{AA}, n_{AT}, n_{TT}\), 단, \(n=n_{AA} + n_{AT} + n_{TT}\)라 한다면 allele A와 T의 빈도 \(f_A, f_T\) 는

\[ \begin{align*} f_A & = & \frac{2n_{AA}+n_{AT}}{2n}, \\ f_T & = &\frac{2n_{TT}+n_{AT}}{2n} \end{align*} \]

로 표현할 수 있습니다. 여기서 세대 t와 세대 t+1의 관계를 살펴보도록 하겠습니다. 세대 t+1의 개체는 세대 t의 집단에서 무작위로 두 사람을 선택해 각각 하나씩의 allele를 물려받게 되지만 이것을 개체가 아닌 세대 t의 allele 집합에서 2개의 allele를 선택하는 것으로 생각할 수도 있습니다. 이 때 세대 t+1의 allele 빈도 \(f_A^{[t+1]}\)는 유전자형 AA에는 두 개, 유전자형 AT에는 한 개가 포함되므로

\[ \begin{align*} f_A^{[t+1]} & = & \left(f_A^{[t]}\right)^2+\frac{1}{2} \cdot 2f_A^{[t]}f_T^{[t]} \\ & = & f_A^{[t]}\left\{ f_A^{[t]}+f_T^{[t]} \right\} \\ & = & f_A^{[t]} \end{align*} \]

가 성립합니다. 따라서 세대 t도 세대 t+1도 같은 allele 빈도를 가지게 되므로 allele의 분포는 대를 거듭해도 평형상태를 이루게 됨을 확인할 수 있습니다. 즉, HWE 법칙은 대를 거듭하더라도 allele 집합에서 각 allele의 빈도가 변하지 않고 평형상태를 유지한다는 법칙을 말합니다.

만약 분석대상이 되는 집단에 대해 임의교배를 가정할 수 있다면 관측된 SNP는 HWE 상태에 있다고 생각할 수 있습니다. 만약 실제로 관측된 유전자형 빈도와 이론적으로 구할 수 있는 기대 유전자형 빈도의 차가 크다면 HWE 법칙을 따르지 않는다고 생각하며 다음의 카이제곱 통계량

\[ \frac{\left\{n_{AA}-n f_A^2 \right\}^2}{n f_A^2} + \frac{\left\{n_{AT}-2n f_A f_T \right\}^2}{2n f_A f_T} + \frac{\left\{ n_{TT}-n f_T^2 \right\}^2}{n f_T^2} \sim \chi^2(df=1) \]

을 이용하여 적합도 검정을 할 수 있습니다.

HWE 법칙을 따르지 않는 원인은 다음과 같은 경우를 생각할 수 있습니다
(1) 하나의 가계에서 추출한 집단
(2) 근친혼의 개체를 포함한 집단(inbreeding)
(3) 비슷한 형질의 개체끼리 결혼을 포함한 집단(assortative mating)
(4) 서로 다른 인종이 섞여 있는 집단
(5) 데이터의 오류

(1)~(3)은 무작위 교배를 가정하는 것이 부자연스러운 집단이므로 HWE 법칙을 가정하는 것 자체가 성립되지 않고, (4)는 집단의 구조화 문제라 부르며 이후 포스팅에서 자세히 알아보도록 하겠습니다. 실제로 무작위 교배를 가정할 수 있는 집단에서 HWE 법칙을 따르지 않는 좌위는 데이터에 오류가 있는 경우가 대부분입니다.

첫 번째 글에서 소개한 바와 같이 이러한 데이터의 오류는 무작위로 일어나는 것이 아닙니다. DNA chip을 이용한 관측에서는 관측기기로부터의 빛의 색으로 유전자형을 결정하게 됩니다. 예를 들어 유전자형이 allele A를 포함하고 있다면 빨강으로 allele T를 포함하고 있다면 녹색으로 빛을 발하게 됩니다. 그러므로 유전자형이 AA일 때는 빨강으로 TT일 때는 녹색으로 AT일 때는 그 혼합인 노란색으로 빛을 발하게 됩니다. AA와 TT에 대해서는 다르게 판단하는 경우가 거의 없지만, AT를 AA 혹은 TT로 판단하는 오류에는 경험상 방향성이 있는 경우가 많습니다. 이러한 오류는 HWE 법칙으로 부터 이탈하는지의 여부로 검출할 수 있으며, GWAS에서는 HWE 법칙을 따르지 않는 SNP는 분석대상에서 제외합니다.

이처럼 가계정보가 없으므로 각 개체의 유전자형을 평가하는 것은 어렵지만, 집단단위로 유전계승법칙에의 적합성을 평가할 수 있는 것이 안정된 분석결과를 유도할 수 있는 하나의 요인이기도 합니다. 단, 상동염색체와 성염색체에서의 HWE법칙의 적용방법은 다름에 주의해야 합니다. 성염색체 중 X 염색체는 어머니로부터는 아들, 딸 어느 쪽으로도 전달될 수 있지만, 아버지로부터는 반드시 딸에게만 전달된다는 것을 고려하여 평가할 필요가 있습니다. 이 X 염색체의 allele 전달에 대해서는 Feller의 저서 제5장 중 “Application to Genetics”와 “Sex-Linked characters”를 참고하기 바랍니다.