GWAS로 배우는 유전통계학 - 2.2 집단의 구조화 문제

2012-04-01
EIGENSTRAT Genomic control GWAS 유전통계학 집단의 구조화

많은 데이터분석에서 문제가 되는 것은 분석 대상 집단의 균질성입니다. 이질적인 집단의 혼재는 데이터분석 결과를 해석하는 데 있어 곤란을 불러일으킬 뿐만 아니라 잘못된 결론을 유도하게 할 수도 있습니다. 그러나 그룹 정보가 없는 데이터의 균질화는 어려우므로 관측항목에 이질성의 원인이 포함되어 있다 가정하고 군집분석 등의 분류모형을 이용해 추정하는 것이 일반적인 방법입니다.

게놈데이터 분석에서 분석 대상 집단의 이질성 대부분은 인종 차이가 그 원인입니다. 게놈연구에서는 이것을 집단의 구조화(population structure)라 합니다. 이번 포스팅에서는 GWAS에서 집단구조화가 분석결과에 미치는 영향, 구조화의 탐색방법, 그리고 그 해결방법에 대해서 알아보도록 하겠습니다.

2.2 집단의 구조화 문제

지금은 국제결혼이 그리 드문 일이 아니지만, 지금까지 인류는 같은 인종끼리 결혼을 하고 자손을 남기는 것이 보통이었습니다. 그 때문에 유전학적으로 보자면 인종 내에서의 allele 빈도는 평형상태에 있었다고 볼 수 있습니다(하디-베인베크르 평형상태; HWE 상태). 그러나 인종에 따라서 그 평형상태는 서로 다른 경우가 대부분이겠죠. 예를 들어 어떤 SNP에 존재하는 2개의 allele A, a에 대해 allele A의 빈도를 백인은 0.2, 흑인은 0.8이라 해보겠습니다. 만약 각각의 인종에 대해 HWE 상태에 있다고 가정하면 각 인종의 유전자형 빈도의 기댓값은 표 1, 표 2가 될 것입니다.

표 1. 백인의 유전자형 빈도, allele A의 빈도가 0.2일 경우

표 2. 흑인의 유전자형 빈도, allele A의 빈도가 0.8일 경우

여기서 만일 1:1의 비율로 두 인종이 섞여 있다고 하면 이 혼합집단의 유전자형 빈도의 기댓값은 표 3이 됩니다. 이 경우엔 HWE 상태에서 벗어나게 되고 보통 분석대상에서 제외하게 됩니다.

표 3. 백인과 흑인이 1:1 비율로 혼합된 집단의 유전자형 빈도

복수의 인종이 섞여 평형상태에 이르기까지는 적어도 수 세대의 무작위 교배가 반복되어야만 합니다. 미국, 유럽은 다민족 국가이기 때문에 아직 평형상태에 이를 때까지 교배가 이루어졌다고는 말하기 어려울 것 같습니다. 그래서 미국, 유럽인 대상의 게놈연구에서는 집단 구조화의 문제가 자주 발생합니다.

반면 동양인은 집단구조화가 적다고 여겨지고 있습니다만, 민족 간 차이가 엄연히 존재하는 것도 사실입니다. 제가 일본에서 직장 생활을 하므로 주로 일본인이 분석 대상이 되는데 일본계 혼혈 아시아인이 포함되는 경우가 간혹 있습니다. 이럴 때는 자료수집 단계에서 출생지를 알 수 있는 정보가 있으면 좋겠지만, 겉모습만으로는 구별이 안 되죠. 게다가 요즘 개인정보 보호 및 인종차별 문제 때문에 실제로 물어보기도 어렵습니다.

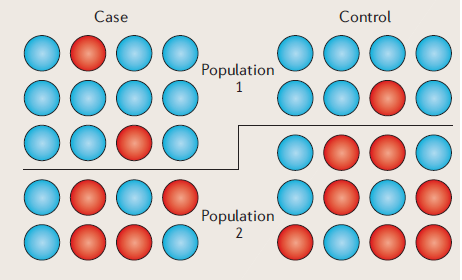
집단구조화 (from Balding, Nat. Rev. Genet, 2006)

Genomic Control

관측 데이터가 어느 정도 이질성을 포함하고 있는지 알아보는 지표 중에 Genomic control(GC)라는 값이 있습니다. GC 값은 집단구조화의 크기를 나타내는 지표로써 각 SNP에서 계산된 Armitage 검정의 중앙값(median)을 그 기댓값인 자유도 1의 카이제곱 분포 값으로 나눈 값 \(\lambda\)을 이용합니다.

\[ \lambda = \frac{median(\chi^2_{obs})}{\chi^2_1 = 0.455} \]

만약 이 값이 1보다 크다면 검정결과 얻어진 카이제곱값을 \(\lambda\)로 보정한 통계량을 이용합니다.

\[ \chi^2_{corrected} = \frac{\chi^2_{obs}}{\lambda} \]

Genomic control은 계산이 간단하다는 장점이 있지만, 모든 SNP에 대해 같은 크기의 보정을 한다는 단점이 있습니다.

주성분 분석을 이용한 방법

한편 GDAS의 게놈정보가 있다면 어느 정도선까지는 인종을 추측할 수 있습니다. HapMap 프로젝트는 나이지리아의 Yoruba 민족(YRP), 동경의 일본인(JPT), 베이징의 중국인(CHE), 미국 유타에 사는 북서유럽의 자손(ECU) 네 집단에 대해 모든 게놈영역에 걸쳐 SNP 좌위를 결정하는 프로젝트입니다. 프로젝트에 이용된 개체의 유전자형 정보가 모두 공개되어 있는데요. 이 정보를 이용해 인종이 불분명한 개체를 분류할 수 있습니다. 전에는 집단의 구조화 문제에 대해 판별분석, 군집분석 등 여러 방법이 사용되었는데 요즘은 주성분분석을 이용한 방법이 주로 사용됩니다. 다음 그림은 HapMap 프로젝트 의해 공개된 중국인 45명과 일본인 44명의 게놈정보 중 약 13만 SNP의 유전자형 데이터를 이용해 주성분분석을 수행한 결과입니다.

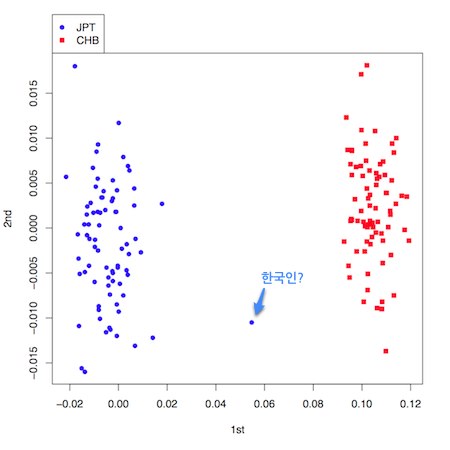
그림으로부터 알 수 있듯이 게놈정보만을 이용한 주성분분석으로 일본인 집단과 중국인 집단을 명확하게 구분하고 있습니다. 실제로 분석을 수행할 때는 일본인을 대상으로 한 연구에서 관측된 개체의 게놈정보와 HapMap 프로젝트의 일본인, 중국인 데이터를 혼합하여 주성분분석을 하고 만약 HapMap 데이터의 일본인 집단으로부터 벗어나는 개체에 대해서는 분석 대상에서 제외하게 됩니다(우리나라에서는 어떻게 하고 있는지 저도 잘 모르겠네요. 어느 분이라도 정보를 주시면 감사하겠습니다).

하지만 게놈정보를 이용한 주성분분석은 통상 통계분석에서 이용하는 주성분분석과는 다른 부분이 있습니다. 바로 데이터의 작성방법에 그 차이가 있는데, \({\bf x_{(i)}} = (x_{i1}, \ldots, x_{in})\), \(i=1,2,\ldots,l\)을 개체 1부터 n까지 \(SNP_i\)의 유전자형 데이터라고 하겠습니다. 여기서 \(n\)은 샘플사이즈, \(l\)은 관측 SNP 수라 하고, 유전자형은 두 개의 allele 중 그 빈도가 작은 allele(minor allele)의 수, 즉, minor allele를 a라고 한다면 AA, Aa, aa를 각각 0, 1, 2로 코딩한 값을 사용합니다. 데이터 행렬을 \(X = {\bf x_{(1)}, x_{(2)}, \ldots, x_{(l)} }\)라 한다면 개체를 분류하기 위해서 통상 \(X^T X\)의 고유벡터로부터 주성분 점수를 계산하게 되는데 \(X^T X\)는 \(l \times l\)의 행렬이 됩니다. 게놈연구는 \(l\)이 보통 50만~200만 정도 되므로 계산량이 엄청나게 많아지게 되기 때문에 게놈 데이터를 이용한 주성분분석에서는 \(n \times n\) 차원의 행렬 \(XX^T\)를 데이터 행렬로 이용하고 이 행렬로부터의 고유벡터를 개체식별 지표로 사용합니다(Price et al, 2006).

다음 포스팅에서는 GWAS를 하기 위해 필요한 그 밖의 데이터 품질평가 방법에 대해 알아보겠습니다.

참고문헌

Armitage P. (1955), Biometrics, 11, 375-386.
Devlin B. and Roeder K. (1999). Biometrics, 55, 4, 997-1004.
The International HapMap Consortium (2003). Nature, 426, 789-796.
Price A.L. et al (2006). Nature Genetics, 38, 905-909