GWAS로 배우는 유전통계학 - 3.2 질적, 양적형질에 대한 관련분석
2012-04-07
Genome-wide association analysis
양적 형질
유전통계학
질적 형질
3.2 질적 형질에 대한 관련분석
질적 형질에 대한 관련분석을 분할표를 이용한 Pearson의 카이제곱 검정이나 Fisher의 정확 검정법을 주로 이용합니다. 어떤 SNP 좌위에 대해 가장 기본적인 관측 데이터는 질적 형질의 표현형에 따른 유전자형의 도수겠죠. 많은 경우 질적 형질은 두 개의 카테고리를 가지므로 개체의 표현형을 D(disease)와 N(non-disease)라 하고 SNP의 allele를 A, a라고 한다면 표 1과 같은 분할표를 작성할 수 있습니다.
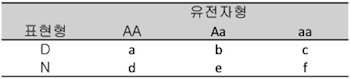
표 1. 유전자형에 따른 돗수의 분할표
이 2×3 분할표에 대해 표현형과 관측 도수 간에 어떠한 관련성이 있는지를 카이제곱 검정 혹은 정확 검정법을 이용해 평가하게 됩니다. 즉, 검정의 귀무가설 “표현형과 유전자형에 따른 도수와는 관련성이 없다”, 대립가설 “표현형과 유전자형에 따른 도수와는 관련성이 있다”에 대한 검정을 하게 됩니다. 만약 검정결과 유의확률(p-value)이 연구 전체의 유의수준(보통 5%)보다 작다면 귀무가설을 기각하게 되고 결과적으로 표현형과 유전자형에는 관련성이 있다고 평가하게 됩니다.
여기서 유전계승양식의 지식을 이용하면 보다 유전학에 따른 분석을 할 수 있게 됩니다. 예를 들어 allele A에 대해 우성양식을 가정한다면 표 1은 표 2와 같이 재구성할 수 있습니다.
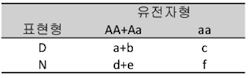
표 2. allele A에 대한 우성양식의 분할표
만약 allele A에 대해 열성양식을 가정한다면 표 3과 같은 분할표를 만들 수 있습니다.
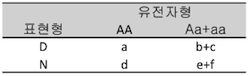
표 3. allele A에 대한 열성양식의 분할표
또한 allele의 도수를 두 군에 대해 비교하는 방법도 가능합니다(표 4).
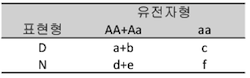
표 4. 표현형과 allele 돗수의 분할표
하지만 병에 걸리는 것은 allele가 아니고 개개인이 되므로 allele 빈도를 이용한 관련분석은 개체를 기초로 하는 분석이 아님에 주의해야 합니다. Allele 빈도를 이용한 관련분석은 검정에 사용되는 표본크기가 유전자형을 이용한 관련분석의 2배가 되므로 검정력(power of test)이 높아지게 됩니다.
우성, 열성, 유전자형, allele 빈도 이외에도 주목하는 allele의 수와 관측 유전자형 돗수사이의 경향성을 이용하여 관련성을 평가하는 방법도 있습니다. 즉, 개체가 보유하고 있는 관심 allele의 수가 질병의 리스크를 높이는가(혹은 낮추는가)에 주목하고 Armitage 검정을 이용하여 경향성의 유무를 평가는 방법입니다.
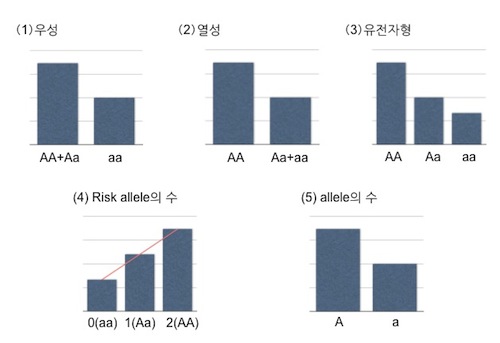
만약 분석 대상이 되는 표현형의 유전계승양식이 알려져지지 않았다면 GWAS에서는 위에서 설명한 5가지 양식 각각에 대한 관련성 평가를 하게 됩니다.
3.3 양적 형질에 대한 관련분석
질적 형질에 대한 관련분석에서는 유전계승양식을 가정하고 각 유전자형 빈도의 차이에 대해 검토하게 됩니다. 또한, 개체의 배경정보(환경정보)가 형질에 미치는 영향을 고려하기 위해 로지스틱 회귀모형 등의 통계모형을 도입해 유전적 요인의 탐색을 하기도 합니다. 실제로 분석 목적에 따라 나이, 성별, 체중, 키 등의 배경정보를 선택합니다.
양적 형질에 대해서도 마찬가지로 형질을 반응변수(목적변수)로 하고 배경정보와 게놈 정보를 설명변수로 하는 회귀모형을 이용한 관련분석을 하는 것이 일반적입니다.
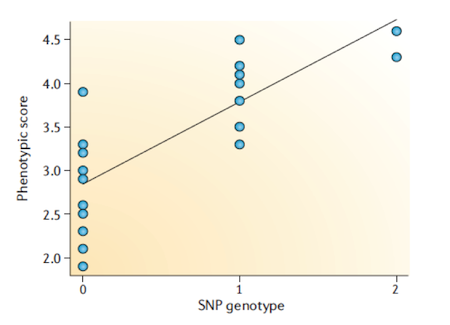
from Balding (2006), Nat. Rev. Genet
예를 들어, 개체의 배경정보를 나이(age), 성별(gender)이라고 하면 양적 형질에 대한 선형모형은
과 같이 표현할 수 있습니다. 여기서 실제로 사용하는 SNP의 값은 유전계승양식에 따라 숫자로 코딩한 값을 입력합니다. 그리고, SNP에 대한 회귀계수에 주목하여 최소제곱법에 의해 추정된 (beta_3) 값에 대한 평가를 합니다. 회귀계수에 대한 검정은 “추정된 회귀계수가 0 인가? (귀무가설)”, “0 이 아닌가? (대립가설)”에 대한 평가가 됩니다.
앞에서 통계모형을 도입해서 분석할 때, 유전자형을 유전계승양식에 따라 숫자로 코딩한 값을 사용한다 했는데 유전자형이 AA, Aa, aa이고 minor allele를 a라 하면
- 우성: minor allele에 대해 우성양식을 가정하면 AA, Aa, aa를 각각 0, 1, 1로 변환한 값을 모형에 사용합니다. 이때 추정되는 회귀계수는 하나이며 AA의 형질에 대한 영향을 0으로 가정했을 때 minor allele를 하나라도 보유하고 있는 개체(Aa or aa)의 형질에 대한 영향을 추정합니다.
- 열성: minor allele에 대해 열성양식을 가정하면 AA, Aa, aa를 각각 0, 0, 1로 변환한 값을 모형에 사용합니다. 이때 추정되는 회귀계수는 하나이며 되며 AA 혹은 Aa의 형질에 대한 영향을 0으로 가정했을 때 aa의 형질에 대한 영향을 추정합니다.
- 유전자형: 3 가지의 유전자형 AA, Aa, aa를 각각 (0,0), (1,0), (0,1)로 변환한 값을 입력합니다. 이는 세 유전자형에 대해 자유도가 2가 되므로 2차원 값으로 변환할 필요가 있기 때문입니다. 이런 변환방법을 처리대비라고 하는데 이때는 추정되는 회귀계수가 2개가 됩니다. 다음 식과 같이 첫 번째 계수는 유전자형 Aa에 대한 영향, 두 번째 계수는 aa에 대한 영향을 추정합니다.
- 경향성: 3 가지의 유전자형 AA, Aa, aa를 minor allele의 갯수 0, 1, 2로 변환한 값을 사용합니다. 추정되는 회귀계수는 1개로 minor allele가 하나 증가함에 따른 영향을 평가하게 됩니다. 즉, aa가 형질에 미치는 영향은 Aa의 2배라고 가정하는 것과 같습니다.
제가 여기서 든 예는 통계모형을 이용한 가장 간단한 예의 하나에 불과합니다. 양적 형질에 대한 관련분석은 질적 형질과 달리 통계모형을 만드는 데 사용하는 배경정보에 따라 분석 결과에 차이가 있을 수 있고 배경정보와 유전자형, 배경정보와 배경정보 사이에 상호작용(interaction)이 있을 수 있기 때문에 결과의 해석이 복잡해 질수 있습니다. 양적 형질에 대한 관련분석은 아직 개선해야 할 문제들이 산적해 있기 때문에 활발한 연구가 이루어지고 있습니다.
통계모형을 이용한 분석이 왜 어려운지는 다음 인용으로 대신하도록 하겠습니다. ^^;
Essentially, all models are wrong, but some are useful.
– George E. P. Box. Empirical Model-Building and Response Surfaces (1987)
참고문헌
- Balding D.J. (2006), Nature reviews Genetics, 7, 10, 781-791.
- 鎌谷直之 (2007) 遺伝統計学入門, 岩波書店 (카마타니 나오유키 (2007), 유전통계학 입문, 이와나미서점 )