GWAS로 배우는 유전통계학 - 5 분석결과의 시각화
2012-04-12
Genome-wide association analysis
Manhattan plot
qq-plot
유전통계학
5. 분석결과의 시각화
GWAS로부터의 검정결과는 분석에 사용하는 DNA chip에 따라 차이가 있지만 보통 50만~150만의 p-값이 계산되므로 그 결과를 하나하나 확인하는 것은 사실상 불가능합니다. 따라서 먼저 시각적으로 분석결과를 확인하고 관련성이 있다고 판단된 SNP좌위의 정보를 확인하는 것이 일반적입니다. 분석결과의 시각화방법으로는 qq-plot(quantile-quantile plot)과 Manhattan plot이 많이 사용됩니다.
Quantile-Quantile plot
만약 분석에 사용된 모든 SNP에 대해 형질과의 관련성에 대해 검정을 할 때 관련성이 없다는 귀무가설이 바르다고 하면 모든 p-값은 0과 1 사이의 균일분포(uniform distribution)를 따르게 될 것입니다. 만약 관련성이 있다는 대립가설이 바르다고 한다면 그때의 p-값은 균일분포로 부터 벗어나게 됩니다.
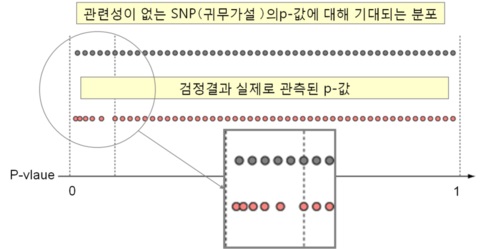
관련성이 있는 SNP가 있다면 그때의 p-값은 이론값보다 작아짐
이 사실을 이용하여 이론적인 분포(균일분포)에서의 p-값과 실제 계산된 p-값을 그래프로 작성한 것이 qq-plot입니다. 즉, 관련성 검정의 대상이 되는 SNP 수를 n, 검정결과 i-번째로 작은 p-값을 $p_{(i)} $라고 하면
(−log10in,−log10p(i)), i=1,⋅,
을 그래프로 그리게 됩니다.
p-값이 작은 부분에서는 형질과 SNP사이에 관련성이 있다는 대립가설에 따른다고 예상되므로 아래 그림과 같이 붉은 원 안의 p-값에 대응하는 SNP가 관련성을 시사하는 SNP가 됩니다.

Manhattan plot
Manhattan plot은 관련분석결과 p-값을 염색체번호, 물리적 거리순으로 늘어놓은 플롯을 말합니다.
여기서 주의해야 할 점은 연쇄불평형(linkage disequilibrium)관계에 있는 SNP 사이의 관련분석 결과는 p-값이 비슷하게 됨에 주목하여 형질과 SNP와의 관련성에 대해 평가해야 합니다. 다시 말해 GWAS에 사용되는 DNA chip은 SNP의 밀도가 높으므로 비슷한 위치에 있는 SNP 사이에는 연쇄불평형 관계가 존재합니다. 이런 때에는 검정의 p-값이 비슷하여지므로 아래 그림과 같이 형질과 관련성이 있는 유전자 영역에 있는 SNP들의 p-값은 고층빌딩과 같이 불쑥 솟아오른 모양이 됩니다1.

참고문헌
- Balding D.J. (2006), Nature reviews Genetics, 7, 10, 781-791.
- 鎌谷直之 (2007) 遺伝統計学入門, 岩波書店 (카마타니 나오유키 (2007), 유전통계학 입문, 이와나미서점 )
그래프의 모양이 맨해튼의 마천루와 비슷하다 하여 Manhattan plot이란 이름이 붙게 되었죠.↩