베이즈 추정을 위한 Stan 맛보기
2014-04-10
R
Stan
시작하며
Bayesian inference using Gibbs sampling:BUGS는 베이즈 추정을 계산기 통계학적으로 수행하는 방법. “계산기 통계학적으로”라는 것은 복잡하고 어려운 함수기술에서 생략할 수 있는 부분은 생략해서 MCMC/Gibbs sampling으로 대체한다는 의미로 생각해도 좋음. 베이즈 추정을 하기 위해 우도 함수 등을 미리 구해 빡시게 코딩하는 것보다는 BUGS(WinBUGS, OpenBUGS, JAGS)등을 이용해 모델의 기술하고 실행한 후 결과를 확인하는 것이 편리. 그렇다고 해도 계산 시간이 오래 걸린다는 문제점은 남아 있음. 여기서는 Stan이라는 최근 많이 사용되는(것 같은?) 소프트웨어를 R에서 사용하는 방법에 대해 메모.
Stan의 개요
Stan의 홈페이지는 여기.
Stan의 개요에 대해서는 이곳과 이곳(일본어)에서 번역 발췌.
모델의 기술방법에 약간의 차이가 있지만, BUGS와 같이 우선 모델을 기술. Stan은 기술된 모델을 일단 C++ 언어로 변환하여 컴파일하는 흐름. C++로 컴파일함으로 인해 고속처리를 기대할 수 있고 일단 컴파일된 모듈을 다른 데이터에도 이용할 수 있게 됨. BUGS에서는 별도의 데이터를 이용하기 위해서는 모델의 확인 -> 데이터 지정 -> 초기화 -> 컴파일의 과정을 전부 다시 해야함. stan을 이용하면 이 과정이 생략되기 때문에 전체 실행 과정의 고속화를 꾀할 수 있음.
또한, C++ 이라는 언어의 특성상 모델의 기술이 엄격하게 되어 데이터의 형태 (int, real) 및 변수가 가질 수 있는 범위를 선언할 수 있게 됨. BUGS에서는 왜 샘플링 에러가 발생했는지 등에 대해 어림짐작으로 대응해야 하기 때문에 경험이 중요했음. 이러한 것들이 구체적으로 지적되기 때문에 디버깅이 편리해짐.
Stan에서 사용하는 난수 샘플링방법은 Hamiltonian Monte Carlo Method를 채용하여 수렴의 속도 및 안정성도 BUGS에 비해 향상됨.
Rstan
환경설정은 이곳을 참조.
기본적인 흐름은
- Rtools을 인스톨하여 CRAN에 등록되지 않은 패키지를 설치할 수 있게함
- Rcpp 패키지 및 inline 패키지을 이용해 Rcpp를 이용한 R의 C++화를 가능하게 하여 stan을 실행.
> install.packages('inline')
> install.packages('Rcpp')> # using library inline to compile a C++ code on the fly
> library(inline)
> library(Rcpp)
> src <- '
+ std::vector<std::string> s;
+ s.push_back("hello");
+ s.push_back("world");
+ return Rcpp::wrap(s);
+ '
> hellofun <- cxxfunction(body = src, includes = '', plugin = 'Rcpp', verbose = FALSE)
> cat(hellofun(), '\n') RStan의 설치
Xcode 5.0.1 + R 3.0.2 + Mac OS X 10.9 (Mavericks) 사용자를 위한 설정
- 실행환경
- Mac OS X 10.9 (Mavericks),
- Xcode toolset 5.0.1 & command-line tools for Mavericks (Xcode와는 별도로 다운로드해야 함)
- R 3.0.3
다음 파일을 만들고
~/.R/Makevars다음 내용을 입력
CXX=g++ -arch x86_64 -ftemplate-depth-256 -stdlib=libstdc++R 에서 다음 코드를 실행
> if (!file.exists("~/.R/Makevars")) {
+ cat('CXX=g++ -arch x86_64 -ftemplate-depth-256 -stdlib=libstdc++\n
+ CXXFLAGS="-mtune=native -O3 -Wall -pedantic -Wconversion"\n',
+ file="~/.R/Makevars");
+ } else {
+ file.show("~/.R/Makevars");
+ }rstan 인스톨
> options(repos = c(getOption("repos"), rstan = "http://wiki.rstan-repo.googlecode.com/git/"))
> install.packages('rstan', type = 'source')rstan을 효율적으로 사용하기 위한 옵션
> library(rstan)
> rstan_options(auto_write = TRUE)
> options(mc.cores = parallel::detectCores())Example
RStan Getting Started의 예제 1번을 따라해보고 제대로 실행 되는가 확인.
> schools_code <- '
+ data {
+ int<lower=0> J; // number of schools
+ real y[J]; // estimated treatment effects
+ real<lower=0> sigma[J]; // s.e. of effect estimates
+ }
+ parameters {
+ real mu;
+ real<lower=0> tau;
+ real eta[J];
+ }
+ transformed parameters {
+ real theta[J];
+ for (j in 1:J)
+ theta[j] <- mu + tau * eta[j];
+ }
+ model {
+ eta ~ normal(0, 1);
+ y ~ normal(theta, sigma);
+ }
+ '
>
> schools_dat <- list(J = 8,
+ y = c(28, 8, -3, 7, -1, 1, 18, 12),
+ sigma = c(15, 10, 16, 11, 9, 11, 10, 18))
>
> fit <- stan(model_code = schools_code, data = schools_dat,
+ iter = 1000, chains = 4)#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:12:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/gevv_vvv_vari.hpp:5:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/var.hpp:7:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/math/tools/config.hpp:13:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/config.hpp:39:
#> /usr/local/lib/R/3.5/site-library/BH/include/boost/config/compiler/clang.hpp:200:11: warning: 'BOOST_NO_CXX11_RVALUE_REFERENCES' macro redefined [-Wmacro-redefined]
#> # define BOOST_NO_CXX11_RVALUE_REFERENCES
#> ^
#> <command line>:6:9: note: previous definition is here
#> #define BOOST_NO_CXX11_RVALUE_REFERENCES 1
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:1:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Core:531:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:2:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/LU:47:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:3:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Cholesky:12:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Jacobi:29:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:3:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Cholesky:43:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/QR:17:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Householder:27:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:5:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/SVD:48:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:6:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Geometry:58:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:14:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/matrix_vari.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat/fun/Eigen_NumTraits.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Dense:7:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Eigenvalues:58:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core.hpp:36:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/core/operator_unary_plus.hpp:7:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/scal/fun/constants.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/math/constants/constants.hpp:13:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/math/tools/convert_from_string.hpp:15:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/lexical_cast.hpp:32:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/lexical_cast/try_lexical_convert.hpp:42:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/lexical_cast/detail/converter_lexical.hpp:52:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/container/container_fwd.hpp:61:
#> /usr/local/lib/R/3.5/site-library/BH/include/boost/container/detail/std_fwd.hpp:27:1: warning: inline namespaces are a C++11 feature [-Wc++11-inline-namespace]
#> BOOST_MOVE_STD_NS_BEG
#> ^
#> /usr/local/lib/R/3.5/site-library/BH/include/boost/move/detail/std_ns_begin.hpp:18:34: note: expanded from macro 'BOOST_MOVE_STD_NS_BEG'
#> #define BOOST_MOVE_STD_NS_BEG _LIBCPP_BEGIN_NAMESPACE_STD
#> ^
#> /Library/Developer/CommandLineTools/usr/include/c++/v1/__config:390:52: note: expanded from macro '_LIBCPP_BEGIN_NAMESPACE_STD'
#> #define _LIBCPP_BEGIN_NAMESPACE_STD namespace std {inline namespace _LIBCPP_NAMESPACE {
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:12:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat.hpp:83:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/csr_extract_u.hpp:6:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Sparse:26:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/SparseCore:66:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:12:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat.hpp:83:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/csr_extract_u.hpp:6:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Sparse:27:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/OrderingMethods:71:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:12:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat.hpp:83:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/csr_extract_u.hpp:6:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Sparse:29:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/SparseCholesky:43:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:12:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat.hpp:83:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/csr_extract_u.hpp:6:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Sparse:32:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/SparseQR:35:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:8:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math.hpp:4:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/rev/mat.hpp:12:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat.hpp:83:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/stan/math/prim/mat/fun/csr_extract_u.hpp:6:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/Sparse:33:
#> In file included from /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/IterativeLinearSolvers:46:
#> /usr/local/lib/R/3.5/site-library/RcppEigen/include/Eigen/src/Core/util/ReenableStupidWarnings.h:10:30: warning: pragma diagnostic pop could not pop, no matching push [-Wunknown-pragmas]
#> #pragma clang diagnostic pop
#> ^
#> In file included from filecf142518d779.cpp:478:
#> In file included from /usr/local/lib/R/3.5/site-library/rstan/include/rstan/rstaninc.hpp:3:
#> In file included from /usr/local/lib/R/3.5/site-library/rstan/include/rstan/stan_fit.hpp:36:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/services/optimize/bfgs.hpp:11:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/optimization/bfgs.hpp:9:
#> In file included from /usr/local/lib/R/3.5/site-library/StanHeaders/include/src/stan/optimization/lbfgs_update.hpp:6:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/circular_buffer.hpp:54:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/circular_buffer/details.hpp:20:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/move/move.hpp:30:
#> In file included from /usr/local/lib/R/3.5/site-library/BH/include/boost/move/iterator.hpp:27:
#> /usr/local/lib/R/3.5/site-library/BH/include/boost/move/detail/iterator_traits.hpp:29:1: warning: inline namespaces are a C++11 feature [-Wc++11-inline-namespace]
#> BOOST_MOVE_STD_NS_BEG
#> ^
#> /usr/local/lib/R/3.5/site-library/BH/include/boost/move/detail/std_ns_begin.hpp:18:34: note: expanded from macro 'BOOST_MOVE_STD_NS_BEG'
#> #define BOOST_MOVE_STD_NS_BEG _LIBCPP_BEGIN_NAMESPACE_STD
#> ^
#> /Library/Developer/CommandLineTools/usr/include/c++/v1/__config:390:52: note: expanded from macro '_LIBCPP_BEGIN_NAMESPACE_STD'
#> #define _LIBCPP_BEGIN_NAMESPACE_STD namespace std {inline namespace _LIBCPP_NAMESPACE {
#> ^
#> 16 warnings generated.> fit2 <- stan(fit = fit, data = schools_dat, iter = 10000, chains = 4)
> print(fit2)#> Inference for Stan model: 31f989ec0d689be2a4996807325a264b.
#> 4 chains, each with iter=10000; warmup=5000; thin=1;
#> post-warmup draws per chain=5000, total post-warmup draws=20000.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> mu 7.91 0.06 5.18 -2.29 4.67 7.90 11.16 18.26 7972 1
#> tau 6.60 0.09 5.79 0.25 2.50 5.23 9.11 20.83 4403 1
#> eta[1] 0.38 0.01 0.93 -1.51 -0.23 0.40 1.01 2.20 20000 1
#> eta[2] 0.00 0.01 0.87 -1.74 -0.56 -0.01 0.56 1.72 20000 1
#> eta[3] -0.19 0.01 0.94 -2.02 -0.82 -0.20 0.44 1.64 20000 1
#> eta[4] -0.03 0.01 0.88 -1.76 -0.61 -0.03 0.55 1.73 20000 1
#> eta[5] -0.34 0.01 0.87 -2.03 -0.92 -0.36 0.22 1.41 20000 1
#> eta[6] -0.21 0.01 0.90 -1.97 -0.80 -0.23 0.36 1.61 20000 1
#> eta[7] 0.34 0.01 0.90 -1.49 -0.24 0.36 0.95 2.07 20000 1
#> eta[8] 0.07 0.01 0.93 -1.76 -0.55 0.08 0.70 1.90 20000 1
#> theta[1] 11.28 0.07 8.22 -2.15 5.97 10.13 15.36 31.22 13697 1
#> theta[2] 7.89 0.04 6.21 -4.52 3.98 7.87 11.72 20.59 20000 1
#> theta[3] 6.23 0.06 7.85 -11.11 2.05 6.73 10.91 21.09 15566 1
#> theta[4] 7.69 0.05 6.51 -5.52 3.71 7.63 11.68 20.79 20000 1
#> theta[5] 5.18 0.04 6.31 -8.72 1.52 5.65 9.34 16.73 20000 1
#> theta[6] 6.12 0.05 6.77 -8.69 2.23 6.51 10.51 18.65 20000 1
#> theta[7] 10.69 0.05 6.82 -1.14 6.05 10.00 14.65 26.06 20000 1
#> theta[8] 8.54 0.07 7.86 -6.92 4.03 8.26 12.79 25.51 13495 1
#> lp__ -4.88 0.03 2.65 -10.75 -6.48 -4.63 -3.01 -0.46 6280 1
#>
#> Samples were drawn using NUTS(diag_e) at Sun Jul 8 20:03:55 2018.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).> plot(fit2)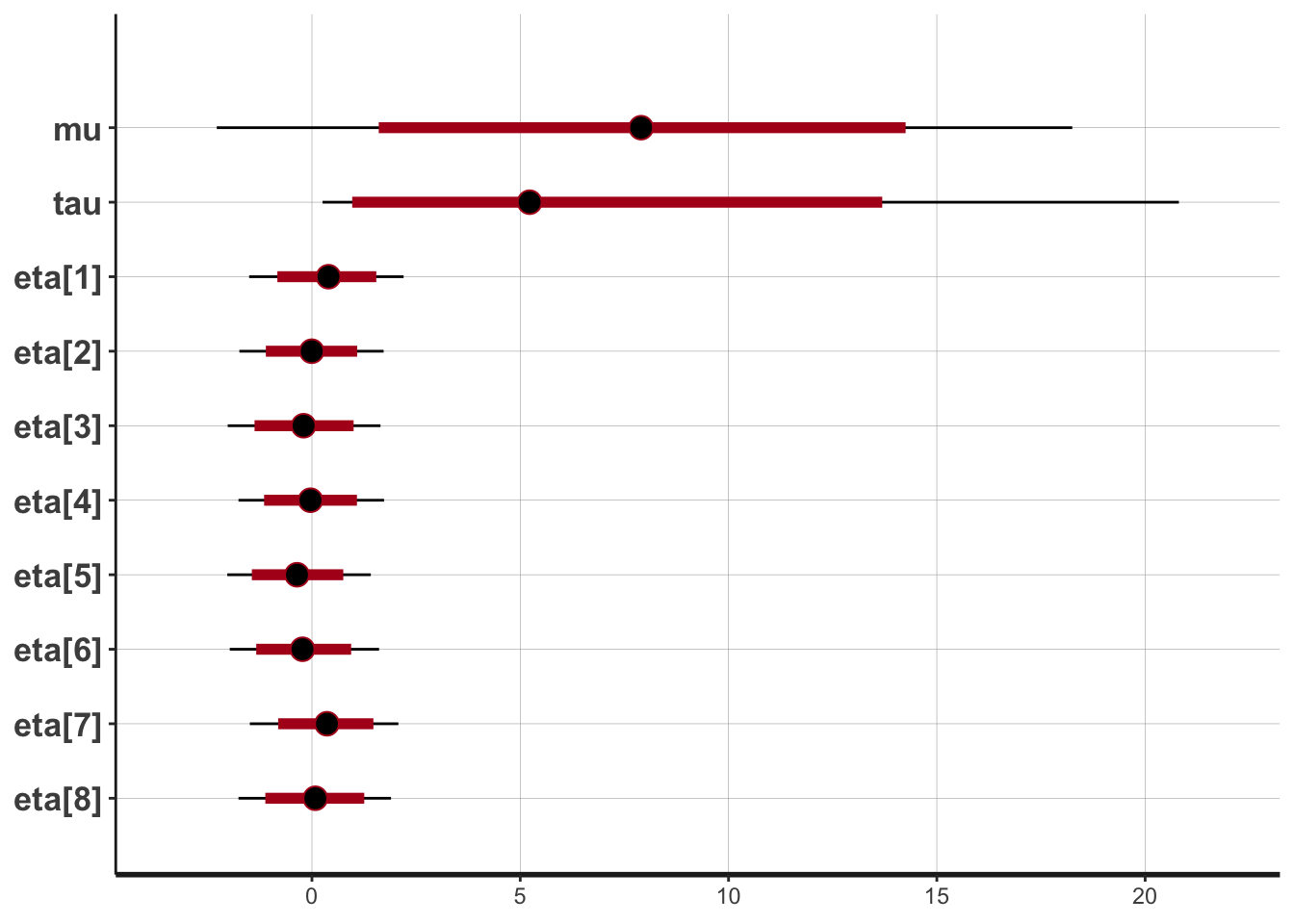
> la <- extract(fit2, permuted = TRUE) # return a list of arrays
> mu <- la$mu
>
> ### return an array of three dimensions: iterations, chains, parameters
> a <- extract(fit2, permuted = FALSE)
>
> ### use S3 functions as.array (or as.matrix) on stanfit objects
> a2 <- as.array(fit2)
> m <- as.matrix(fit2)