rstan을 이용한 베이즈 회귀분석

2018-07-08
rstan regression bayesian

이번 포스트에서는 단순 회귀분석의 예를 통해 Stan과 rstan의 사용법을 알아본다. 실제로 R에서 Stan을 실행하여 MCMC 샘플을 얻어서 베이즈 신뢰구간 및 베이즈 예측구간을 계산한다.

데이터 분포 확인

예제로 R에 포함된 cars 데이터를 이용한다. 이 데이터는 자동차의 속도 speed (mph)와 제동거리 dist 를 측정한 데이터로 50개의 관측값이 들어있다.

> library(tidyverse)
> ggplot(cars, aes(x = speed, y = dist)) +
+   geom_point() +
+   geom_smooth(method='lm') +
+   theme_minimal()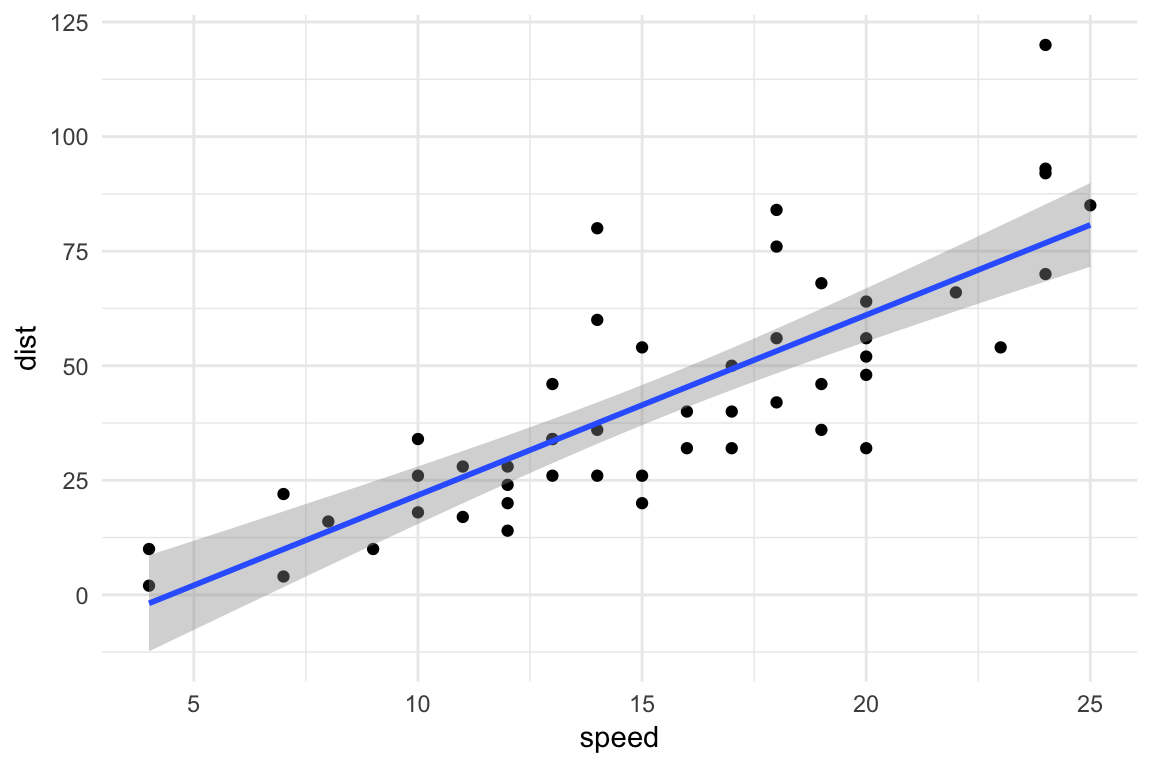

이 데이터의 산점도를 통해 자동차의 속도가 빠를수록 제동거리가 늘어나는 양의 상관관계가 존재하며 회귀분석에 적합한 데이터임을 알 수 있다.

모형식의 기술

단순회귀식은 다음과 같다.

\[ Y[n] = a + bX[n] + \epsilon[n], \\ \epsilon[n] \sim Normal(0, \sigma), ~~n = 1, \ldots, N \]

이 식을 다른 형태로 변환하면

\[ Y[n] \sim Normal(a + bX[n], \sigma), ~~n = 1, \ldots, N \] 로도 표현할 수 있다.

lm 함수를 이용한 추정

> lm_model <- lm(dist ~ speed, data = cars)
> summary(lm_model)
#> 
#> Call:
#> lm(formula = dist ~ speed, data = cars)
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#> -29.07  -9.53  -2.27   9.21  43.20 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)
#> (Intercept)  -17.579      6.758   -2.60    0.012
#> speed          3.932      0.416    9.46  1.5e-12
#> 
#> Residual standard error: 15.4 on 48 degrees of freedom
#> Multiple R-squared:  0.651,  Adjusted R-squared:  0.644 
#> F-statistic: 89.6 on 1 and 48 DF,  p-value: 1.49e-12
> library(rstan)
> library(ggmcmc)

Rstan을 이용한 추정

Stan 코드 작성

data {
  int N;
  real X[N];
  real Y[N];
}
parameters {
  real a;
  real b;
  real<lower = 0> sigma;
}
model {
  for (n in 1:N) {
    Y[n] ~ normal(a + b * X[n], sigma);
  }
}

Stan 코드의 기본 구성은 data, parameters, model 3개의 블록으로 되어있다. data 블록에서는 관측 데이터를 선언하고 parameters 블록에는 샘플링하고 싶은 모수를 선언한다. model 블록에는 우도(likelihood)와 사전분포(prior distribution)를 기술한다.

예제 코드에서는 각 모수의 무정보 사전분포의 기술을 생략했다. 사전분포를 지정하지 않으면 Stan은 자동으로 제한된 범위 안에서 충분히 넓은 폭의 uniform 분포를 사용한다.

Stan 코드는 1) 별도의 파일로 저장, 2) R 코드 안에서 정의, 3) R Markdown 문서 안에 포함 시키는 방법 등을 이용해 기술할 수 있다. 이 포스트에서는 3)을 이용해 simple_reg라는 이름의 stanmodel 객체로 컴파일한 결과를 R에 넘기는 방법을 사용했다.

R 코드의 구성

> rstan_options(auto_write = TRUE)
> options(mc.cores = parallel::detectCores())
> 
> fit <- sampling(simple_reg,
+                 data = list(N = nrow(cars), X = cars$speed, Y = cars$dist), 
+                 seed = 34)
> save(fit, file = "rlt-simple-reg.RData")

함수 sampling은 컴파일된 stanmodel을 이용해 MCMC 샘플링을 실행한다. fit는 stanfit 이라는 클래스의 객체로 MCMC 설정과 추정결과물인 MCMC 샘플을 보존하고 있다. 때때로 MCMC 추정에 오랜 시간이 걸릴 경우도 있으니 추정된 샘플을 별도 파일로 저장하는 것을 추천한다.

RStan 결과

> load("rlt-simple-reg.RData")
> class(fit)
#> [1] "stanfit"
#> attr(,"package")
#> [1] "rstan"
> fit
#> Inference for Stan model: stan-6a5959936849.
#> 4 chains, each with iter=2000; warmup=1000; thin=1; 
#> post-warmup draws per chain=1000, total post-warmup draws=4000.
#> 
#>          mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff
#> a      -17.47    0.19 7.16  -31.68  -22.20  -17.54  -12.57   -3.91  1398
#> b        3.93    0.01 0.44    3.07    3.63    3.93    4.22    4.80  1411
#> sigma   15.81    0.04 1.64   12.99   14.66   15.67   16.82   19.41  2119
#> lp__  -159.48    0.04 1.29 -162.96 -160.02 -159.15 -158.55 -158.03  1055
#>       Rhat
#> a        1
#> b        1
#> sigma    1
#> lp__     1
#> 
#> Samples were drawn using NUTS(diag_e) at Sun Jul  8 15:03:38 2018.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at 
#> convergence, Rhat=1).

예제 실행 후 얻어진 MCMC 샘플의 수는 chains * (iteration - warmup) / thin 으로 4 * (2000 - 1000) /1 = 40000 며, 위 출력의 6~15번째 줄이 샘플링한 각 모수에 대한 요약 통계치이다.

요약 통계치의 첫번째 열은 모수의 이름이다. Stan은 사후확률이 높은 곳을 효율적으로 탐색하기 위해 로그를 취한 사후확률 \(\log p(\theta | Y) = \log p(Y|\theta) + \log p(\theta) + const\)을 모수 \(\theta\)에 대해 편미분 한 값을 사용한다. 이를 위해 각 MCMC 스텝의 모수 \(\theta^*\)에 대한 \(\log p(Y|\theta^*) + \log p(\theta^*)\)의 값을 lp__(log posterior)라는 이름으로 내부에 저장한다. lp__도 다른 모수와 마찬가지로 수렴해야 한다.

maen은 MCMC 샘플의 사후평균(posterior mean) 이며 이 값이 lm 함수를 이용하여 추정한 모수 값과 큰 차이가 없음을 확인할 수 있다. se_eman은 mean의 표준오차이며 MCMC 샘플의 분산을 n_eff로 나눈값이다. sd는 MCMC 샘플의 표준편차이다. 2.5% ~ 97.5%는 MCMC 샘플의 분위 수이며 베이즈 신뢰구간 혹은 베이즈 예측구간이다. n_eff는 Stan이 자기 상관(auto correlation) 등으로 부터 판단한 유효 MCMC 샘플의 수이다. 이 값이 작으면 모수가 수렴하기 어렵다는 것이므로 모형 개선이 필요하다는 힌트가 된다. 분포를 추정하거나 통계량을 산출하기 위해서는 적어도 100 이상의 값이 바람직하다. Rhat은 MCMC가 수렴했는가를 알려주는 지표로 “Chain 수가 3이상이며 모든 모수의 \(Rhat < 1.1\) 이면 수렴했다 할 수 있다”라고 판단하며 모든 모수가 수렴할 때까지 모델 구축의 시행착오를 반복해야 한다. 자세한 것은 Bayesian Data Analysis를 참조.

수렴진단

> fit_ggs <- ggs(fit, stan_include_auxiliar = TRUE)
> ggs_traceplot(fit_ggs) +
+   theme_minimal()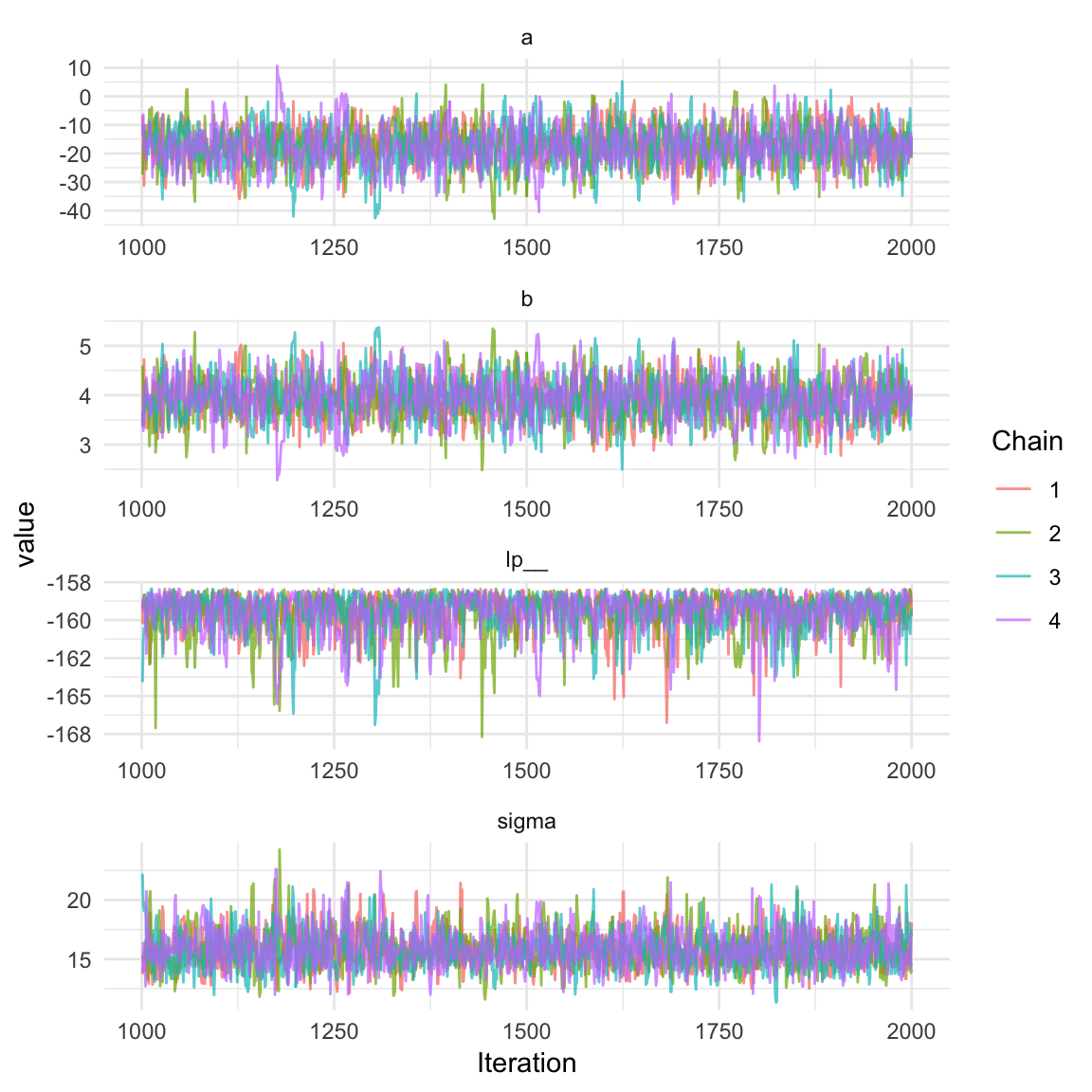

ggmcmc 패키지는 trace plot을 이용한 수렴진단을 할 때 유용하다. Rstan에도 진단을 위한 그래픽 작성 함수가 포함되어 있지만, 모수가 많을 때 그래프를 통한 확인이 어려울 때가 있다. 함수 ggs는 stanfit 객체를 data.frame으로 변환하는 역할을 한다. 만약 warmup의 결과도 확인하고 싶다면

> fit_ggs <- ggs(fit, inc_warmup = TRUE)

와 같이 기술한다. stan_include_auxiliar = TRUE는 lp__의 추정값을 추출하기 위한 옵션이다.

comments powered by Disqus